Grafräknare - Grafräknarfunktioner

Matematisk analys

Skriv ut

Identifiera skärningspunkten mellan 2 kurvor

Låt säga att vi ska lösa olikheten grafiskt och svara med två gällande siffror.

Vi börjar med att skriva in de båda funktionerna y=x^1,2 och y=3-x på grafräknaren.

FLERA BILDER
FLERA BILDER
FLERA BILDER

Vi får då en graf som ser ut så här:

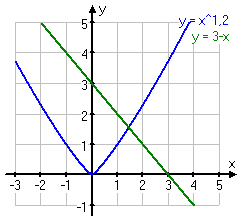
Lösningen, alltså värdet på x, finns där de båda kurvorna möter varandra. Klicka på 2nd-knappen och sedan knappen ”TRACE” vilket gör att vi får valet ”CALC” som står ovanför.

Här bläddrar vi nu ner till nr 5 ”intersect” som ska hjälpa oss att beräkna skärningspunkten, alltså var någonstans kurvorna korsar varandra. På skärmen får vi nu fram följande bild:

Här ovan ser vi nu att den kurva som är markerad är den som anges i övre vänstra hörnet, det är alltså på den som vår lille markör befinner sig på just nu. Vi ser också på skärmen att grafräknaren frågar efter den första kurva som är med och bildar skärningspunkten som ska beräknas. Den vill alltså att vi med vår markör ska markera den punkt på första kurvan som är så nära skärningspunkten som möjligt. Du förflyttar pricken längs kurvan med hjälp av höger och vänster pil.

När du tycker att du har passat in pricken med punkten där kurvorna möts så klickar du ”ENTER”. Och följaktligen får vi fram nästa skärmbild som du ser här nedanför:

Vi ser här att den kurva som är markerad nu är y=3-x och det är på den som vår markör nu är fäst. Grafräknaren frågar denna gång efter den andra kurvan som är med och bildar skärningspunkten. Vi flyttar alltså vår markör med höger och vänster pil och passar in den så bra som möjligt i mötespunkten.

När du känner dig nöjd, klicka ”Enter”. Det sista grafräknaren ber dig göra nu är att gissa var exakt skärningspunkten är. Så flytta runt markören tills du tycker du har träffat mitten och klicka än en gång ”Enter”:

Innan du ens har hunnit blinka så presenterar grafräknaren följande resultat:

Skärningspunkten mellan kurvorna y=x1,2 och y=3-x har koordinaterna (avrundat) x=1,4 och y=1,6.

Hur ska vi då svara? Eftersom detta är en olikhet så är x antingen större än eller mindre än 1,4, men hur vet vi det då? Jo, man kan antingen läsa ut detta grafiskt eller helt enkelt testa sitt svar genom beräkning.

Grafiska utläsningen: Om vi kollar på grafen ovan så ser vi att kurvan x^1,2 är mindre än linjen 3-x ända fram till den punkt x=1,4 där de möts. Alltså, kurvan x^1,2 har ett lägre y-värde än linjen 3-x ända fram till deras skärningspunkt. Då kurvan har passerat linjen så är det den som har större y-värde än linjen. Villkoret som olikheten x^1,2 < 3-x anger är ju att kurvan x^1,2 skulle vara mindre än linjen 3-x och det villkoret uppfyller den kurvan ända fram till precis innan punkten 1,4.
Alltså blir vårt svar att x < 1,4, för det är då olikheten är sann. x får inte vara lika med 1,4 för i den punkten har de båda graferna samma värde och det är ju inte det som olikheten talar om för oss eller hur?

Uträkningen: Om ni tycker att det är klurigt att läsa ut detta ur en graf så kan ni istället helt enkelt testa er lösning. Vi har två lösningar att välja mellan: x < 1,4 och x > 1,4.

För att testa om x är större än 1,4 är rätt så tar vi helt enkelt ett värde som är större än 1,4 t.ex. 1,5 och sätter in det i olikheten:

testas:

Som ni ser så är ju inte alls 1,63 mindre än 1,5, vilket innebär att denna lösning är fel.

Då testar vi istället x<1,4 och väljer då ett värde som är mindre än 1,4 t.ex. 1 och så sätter vi in det i olikheten:

testas:

Denna gång stämmer det då 1 faktiskt är mindre än 1,7, och därmed kan vi konstatera att svaret blir x < 1,4.
[/example]

Räkna ut värdet på en derivata

Först och främst så vill jag bara säga att det är viktigt att du även kan räkna ut sådan här på papper eftersom man oftast måste redovisa hela uträkningen. Det skadar dock inte att kunna räkna ut en derivata på miniräknaren eftersom det är en utmärkt referens till det rätta svaret, alltså så att man vet vad för svar man borde komma fram till.

Låt säga att vi har en uppgift där funktionen y(x)=4x² är angiven. Uppgiften vill att du ska beräkna y’(3).

1. Gå in på och bläddra sedan ner till alternativ nr 8, nDeriv( (engelska) derivata( (svenska), klicka enter. (Istället för att bläddra med pilarna kan du helt enkelt trycka 8.)

⇒

2. Då börjar vi med att skriva in vår funktion som ska deriveras.

3. För att markera att funktionen är färdigskriven så sätter vi ett komma som en avskiljare ()

4. Därefter anger vi variabeln som ju är x , och sedan ännu ett komma.

5. Det sista vi anger innan vi avslutar parentesen är värdet på x som i detta fall skulle vara 3. Sedan är det bara att trycka enter och vi får svaret 24 på y’(3).

Minnesregel
Då vi räknar ut en deriverad funktions värde då värdet på x är angivet skriver vi följande:

(Observera att det inte ska vara något mellanslag mellan komma och ord, jag har det bara för att det ska vara tydlig text.)

Räkna ut värdet på en integral

Först och främst så vill jag bara säga att det är viktigt att du även kan räkna ut sådan här på papper eftersom man oftast måste redovisa hela uträkningen. Det skadar dock inte att kunna räkna ut en integral på grafräknaren eftersom det är en utmärkt referens till det rätta svaret, alltså så att man vet vad för svar man borde komma fram till.

Låt säga att vi har fått i uppgift att beräkna integralen

1. Gå in på och bläddra sedan ner till alternativ nr 9, fnInt( (engelska) integral( (svenska), klicka enter. (Istället för att bläddra med pilarna kan du helt enkelt trycka 9.)

=>

2. Då börjar vi med att skriva in vår funktion som ska beräknas i integralen.

3. För att markera att funktionen är färdigskriven så sätter vi ett komma som en avskiljare ().

4. Därefter anger vi variabeln som ju är x , och sedan ännu ett komma.

5. Sedan skriver vi dit den undre gränsen, som i detta fall var 0, och därefter lägger vi till ännu ett komma.

6. Sist skriver vi dit den övre gränsen, 4, och avslutar sedan parentesen.

Då vi klickar på enter så tar det bara ett ögonblick sedan ger grafräknaren oss svaret!

Minnesregel
Då vi räknar ut en integrals värde skriver vi följande:

(Observera att det inte ska vara något mellanslag mellan komma och ord, jag har det bara för att det ska vara tydlig text.)

Anpassa en funktion till observerade data

Som nämnt på sidan om Modellering så innebär funktionsanpassning till observerade data en regressionsanalys.

Det finns flera olika funktioner man kan välja mellan, men arbetssättet är dock gemensamt för dem alla. Vi kommer att arbeta efter följande steg:

1. Mata in värdena i en tabell i räknaren
2. Välj vilken typ av funktion som du vill anpassa

1. Mata in värdena i en tabell

Tryck på knappen [STAT], du ser att det sedan finns 3 olika undermenyer till STAT nämligen: EDIT, CALC och TESTS. Vi ska hålla oss kvar på EDIT och där välja första alternativet “1:Edit…”. Klicka [ENTER] eller 1 för att välja det första alternativet.

Vi får nu upp en vy med olika listor som grafräknaren använder i olika beräkningar. L1, L2, L3 osv. Beroende på vad man har gjort för beräkningar tidigare så kan det ibland ligga en massa siffror lagrade i dessa listor. Om så är fallet så kan dessa rensas genom att man flyttar markören så den markerar t.ex. L1 och tryck därefter [CLEAR] och tryck sen ner-pilen för att flytta undan markören varpå listan nu har tömts. Upprepa för fler listor om du behöver mer plats. I vårt fall så behöver vi använda oss av L1 och L2.
Nu när första raden i L1 är markerad så kan vi börja föra in x-värdena. Börja skriv första mätvärdet och klicka sen [ENTER] för att lägga till i listan. Upprepa med övriga x-värden. Flytta sedan markören ett steg åt höger för att komma till L2-listan istället. Här matar vi in y-värdena enligt samma metod som för L1.

Välja funktion att anpassa

Gillade du denna sida? Hjälp andra att hitta den!

Genom att trycka på länkarna här över så sprider du ordet om Matteguiden och hjälper oss att växa. På så sätt kan vi fortsätta att hjälpa besökare som behöver hjälp med matten.