Grafräknare - Grafräknarfunktioner
Sannolikhetslära och matematisk statistik
Medelvärde, median och standardavvikelse
Simulera slumpförsök med heltal
Med hjälp av grafräknarfunktionen RandInt kan man simulera försök som t.ex. när man kastar en tärning eller ett mynt x antal gånger. Funktionen innebär att grafräknaren slumpar fram tal i ett visst intervall (1-6 för tärningen, 1-2 för myntet med krona/klave) så många gånger som du anger. Det fungerar helt enkelt som en slumpgenerator för heltal.
Börja med att gå in MATH och bläddra till fliken PRB. På femteplats hittar du “RandInt”. För grafräknare med svenska som språk så är det fliken SAN ni ska bläddra till och på femteplats står det där “slumpHeltal”. Infoga genom att klicka enter då ni markerat alternativet.
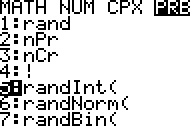
I RandInt( fyller man sedan i intervallet med siffror som den ska slumpa fram. Om vi ska simulera att man kastar ett mynt så kan det ju antingen bli krona eller klave. Två alternativ där kronan t.ex. kan motsvara ettan och klave kan motsvara tvåan. Vi skriver intervallet 1-2 genom att separera siffrorna med ett kommatecken. Sedan ska vi ange hur många gånger vi vill utföra försöket. Låt säga att vi singlar slanten 100 gånger. Skriv in 100 genom att skilja det med ett kommatecken från intervallet. Avsluta parentesen.
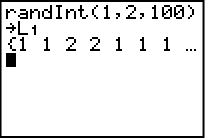
Om vi nu skulle klicka enter så skulle vi få en lång radda med tal, det är ganska osmidigt att sitta och räkna hur många ettor och tvåor vi har fått på hundra slantsinglingar. Men vi kan på ett smidigt sätt få reda på detta genom att låta grafräknaren presentera resultatet i ett stapeldiagram.
Efter att vi har avslutat parentesen lägger vi alltså till ett kommando som gör att talserien sparas i en lista, förslagsvis L1. Klicka på knappen STO> för att få pilen som “hänvisar” ett resultat till det som står efter den. L1 infogar vi genom att klicka 2ND och sedan 1 på grafräknaren (L1 står med blå text ovanför denna knapp).
Nu klickar vi enter. Alla försök visas på rad, men resultatet har även sparats till L1. Nu vill vi att L1 ska visas i en graf med staplar.
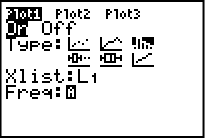
Klicka på 2ND och sedan knappen Y= för att komma åt funktionen “STAT PLOT”. Ni får då upp denna bild:
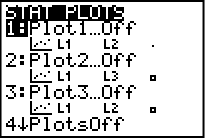
Klicka enter när den översta är markerad. Vi kommer nu till bilden nedan. Vi ändrar i inställningarna så att grafen är “On”, visar staplar och x-list = L1 genom att markera alternativen och klicka enter. Freq behöver ni inte göra något med.
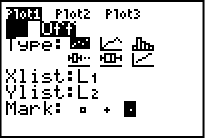
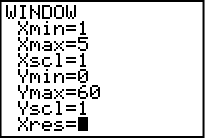
Vi klickar oss vidare med knappen WINDOWS för att ställa in fönstret. Fyll i de värden som syns i bilden. Vi angav ju intervallet 1-2, med andra ord behöver vi inte se så mycket mer på X-axeln. Vi gjorde hundra kastningar (om krona och klave får lika många så det blir 50+50) så vi borde åtminstone sätta y-axeln till 60, detta går ju att ändra på sedan om inte bilden blir bra. Xres = 1.
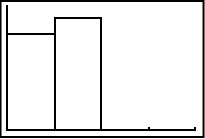
Klicka sedan på knappen GRAPH och din grafräknare ritar snyggt upp två staplar. Den första stapeln står för hur många gånger en etta slumpades fram, den andra stapeln står för hur många gånger en tvåa slumpades fram.
Genom att klicka på knappen TRACE så markeras den första stapeln och vi ser att grafräknaren anger antalet gånger det blev en etta, n = 46. Flytta markören ett steg åt höger med pilarna så hoppar den till stapel två där vi ser att antalet gånger som det blev en tvåa var 54 gånger.
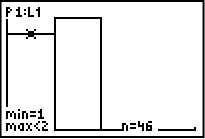
Så om vi ska besvara vad sannolikheten är att vi får klave (som motsvarade talet 2 på grafräknare) så kan vi svara att i ett försök med 100 slantsinglingar så blev det klave i av fallen jämfört med det teoretiska värdet på 50%.
Beräkna a-uppgiften i exempel 2 med hjälp av din grafräknare.
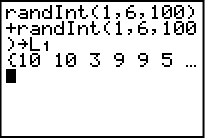
Vi simulerar tärningskastet med de två tärningarna med hjälp av RandInt. Infoga RandInt och skriv in intervallet 1-6 då det är de siffror som finns på en tärning. Vi gör försöket 100 gånger.
NOTERA att det är två tärningar, vars resultat vi ska summera, som vi kastar. Med andra ord måste vi skriva in samma sak en gång till och lägga ihop den med den andra tärningen (summera). Skriv sedan dit en pil och därefter L1 för att få resultatet sparat i listan. Klicka enter.
Vi går vidare och gör de nödvändiga inställningarna via STAT PLOT för att få fram ett stapeldiagram.


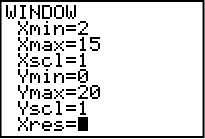
Klicka sedan på WINDOWS för att ställa in fönstret. Summan för två tärningar sträcker sig från 2 (1+1) till 12 (6+6) så vi ställer in intervallet 2-15 på x-axeln. Y-axeln räcker med 20 som max då det är så många staplar som de hundra kasten kan fördela sig på.
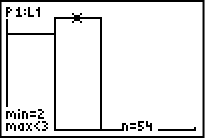
Klicka sedan på GRAPH och du får den här bilden:
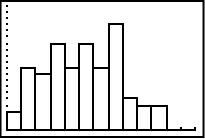
Klicka på TRACE och skriv sedan ner värdet på n för respektive stapel som uppfyller kravet att summan är 6 eller mindre.
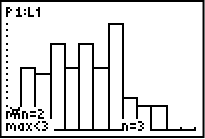
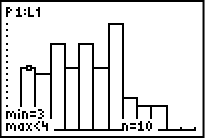
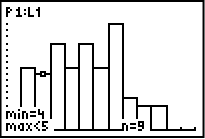
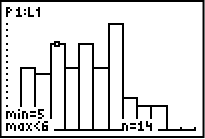
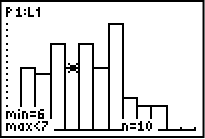
Vi lägger samman alla tal vi får ut:
I detta slumpförsök så resulterade alltså 46 kast av 100 kast i att summan av tärningarna blev 6 eller mindre. Med andra ord skedde detta i 46% av fallen jämfört med det teoretiska värdet på 42%.
Svar: Sannolikheten är 46%.