Matte 1 - Funktioner
En linjes lutning och ekvation
Vi kan illustrera olika linjära samband mellan två variabler i ett koordinatsystem genom att rita en rät linje. Då vi beskriver en rät linje i ett koordinatsystem så kan det vara bra att studera linjens lutning.
Först ska vi definiera när en linje lutar uppåt respektive neråt. Vi tittar helt enkelt från vänster till höger och där kan linjen alltså luta uppåt eller neråt.
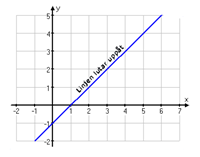
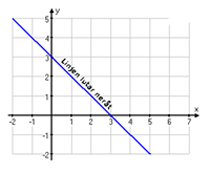
Det tal som bestämmer hur mycket linjen lutar kallas för linjens riktingskoefficient. Den berättar hur stor ändring det blir i y-led då man tar ett steg åt höger i x-led. Då vi flyttar oss ett steg åt höger på x-axeln och sedan rör oss uppåt i y-led för att fortfarande följa linjen, så är riktningskoefficienten positiv. Rör vi oss istället neråt för att följa linjen så är den negativ.
I enkla fall så behöver vi bara räkna rutorna i koordinatsystemet för att beräkna riktningskoefficienten.
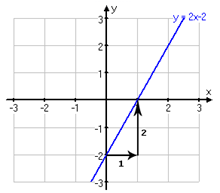
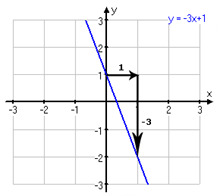
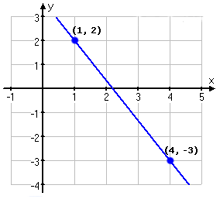
Ett steg åt höger, två steg uppåt. Riktningskoefficienten är 2.
Ett steg åt höger, tre steg nedåt. Riktningskoefficienten är -3.
Däremot så går det inte alltid att bestämma riktningskoefficienten genom att räkna rutor. Därför finns det en formel vi kan använda oss av då vi vet två punkter där linjen passerar i koordinatsystemet.
Riktningskoefficienten k för en linje kan beräknas genom
med hjälp av punkterna och som linjen går genom.
Bestäm riktningskoefficienten för den linje som går genom punkterna och
Notera att det inte spelar någon roll vilken punkt du börjar med:
k-form
Det är dags att lära sig hur man skriver upp en ekvation för en linje. Denna ekvation sägs vara skriven i k-form.
y = kx + m är en linjes ekvation i k-form. k är linjens riktningskoefficient och m är y-koordinaten för linjens skärning med y-axeln.
En rät linje skär y-axeln i punkten och har riktningskoefficienten 2. Vilket samband gäller mellan koordinaterna för en godtycklig punkt på linjen?
Vi sätter in de värden vi har i formeln för k:
är alltså ekvationen och sambandet för linjen.
Svar: Sambandet mellan x- och y-koordinaterna är .
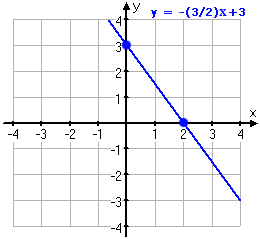
Rita linjen med ekvationen .
Då vi vet att m=3 så kan vi också säga att linjen går igenom punkten , stället där linjen skär y-axeln.
Om vi sedan går 2 steg åt höger och sedan 3 steg neråt så får vi en ny punkt på linjen. Därefter är det bara att dra en linje genom de båda punkterna.
Enpunktsformeln
Om vi vill bestämma en linjes ekvation i k-form och bara har riktningskoefficienten och en punkt given så kan vi använda oss av enpunktsformeln.
där vi vet värdet på k och punkten
Exemplet finns även som videoundervisning >>
En linje har riktningskoefficienten 1,5 och går genom punkten .
Bestäm linjens ekvation i k-form. Vi sätter in de värden vi har i formeln .
Svar: Linjens ekvation är .
En linje genom två punkter
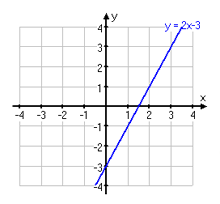 En rät linje passerar genom punkterna och . Bestäm ekvationen för linjen.
En rät linje passerar genom punkterna och . Bestäm ekvationen för linjen.
Först räknar vi ut k.
För att räkna ut m så sätter vi in en av punkterna i ekvationen .
Ex. punkten
Detta ger oss ekvationen .
Svar: Linjens ekvation är .
Allmän form
Då vi skriver en ekvation för en linje i allmän form så skriver vi helt enkelt om ekvationen så att vi får 0 på höger sida.
Skriv ekvationerna och på allmän form.
Flytta över alla termer på vänstersidan och skriv konstanten sist i VL:
Flytta över alla termer på vänstersidan och skriv konstanten sist i VL:
För att få bort nämnarna så kan vi multiplicera alla tal med 15. 15 är det minsta talet som både kan delas med 3 och 5.
15 delas med 5 och kvar blir 3·4. 15 delas med 3 och kvar blir 5·1.
Svar: och
Varje ekvation på formen Ax+By+C=0, där A, B och C är givna tal och B ≠ 0, kan skrivas i formen y = kx + m och är därför ekvationen för en rät linje.
Då vi ska rita linjer i allmän form så är det ofta bra att bestämma skärningspunkterna med koordinataxlarna.
Rita linjen med ekvationen och skriv ekvationen på k-form.
För att kunna rita upp linjen behöver vi 2 koordinater. Förslagsvis kan vi välja koordinaten där x=0 och koordinaten där y=0. Om du sätter att x=0 så kan du lösa ut vad y har för värde i den punkten och tvärtom:
x=0 ger
y=0 ger
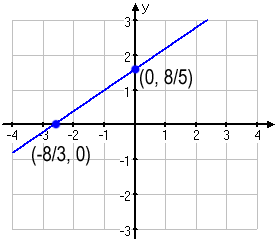 Nu har vi räknat ut koordinaterna för de två punkter där linjen skär koordinataxlarna, nämligen punkterna och . Då återstår det bara att pricka in de två punkterna i koordinatsystemet och dra en linje genom dem.
Nu har vi räknat ut koordinaterna för de två punkter där linjen skär koordinataxlarna, nämligen punkterna och . Då återstår det bara att pricka in de två punkterna i koordinatsystemet och dra en linje genom dem.
Vi skulle även skriva om ekvationen i k-form:
Svar:
Parallella linjer
Två linjer är parallella om dem har samma riktningskoefficient eller båda är parallella med y-axeln.
Bestäm konstanten a i ekvationen så att motsvarande linje är parallell med linjen .
Vi skriver först om dem båda ekvationerna i k-form.
och
Då två linjer är parallella så har de båda samma k-värde. I och med det kan vi sätta respektive ekvations uttryck för k att de är lika med varandra:
På så vis har vi fått en ekvation där vi kan räkna ut konstanten a.
Då x finns i täljaren i både HL och VL så kan vi dividera bort det:
Flytta över fyran till andra sidan så att den hamnar i täljaren i HL:
Svar: