Matte 1 - Geometri
Omkrets och area
Omkrets och area på månghörningar
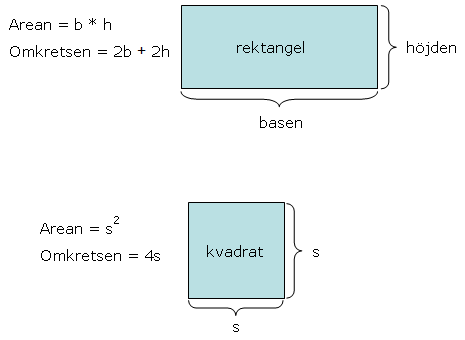
Rektangel
Då vi ska räkna ut arean av en rektangel så multiplicerar vi basen med höjden. Samma sak gör vi med kvadrater som är så kallade liksidiga rektanglar, alltså alla sidorna är lika långa. Detta gör så att kvadratens area är sidan i kvadrat eller sidan upphöjt till 2.
Lille Bosse är ute och gör kullerbyttor på gräsmattan utanför villan han och hans familj bor i. Tomten är rektangulär och har en yta på 1408 m2. Hur bred är tomten om dess längd är 64 meter?
Vi börjar med att rita en figur. Att rita upp det man ska beräkna underlättar mycket och avlastar hjärnan som då kan fokusera mer på beräkningen.
Tomten var rektangulär så vi ritar upp en rektangel och skriver dess area som var 1408 m2. vi fick också reda på att längden (=basen) var 64 meter. Vi ska alltså räkna ut bredden (=höjden) på tomten.
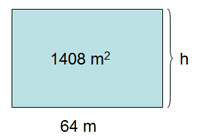
Formeln för arean hos en rektangel säger att basen·höjden=arean. Vi ställer upp den med våra tal som vi vet:
Vi har nu fått en ekvation där vi lätt kan lösa ut h och därmed få reda på bredden.
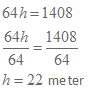
Svar: Tomten är 22 meter bred.
Parallellogram
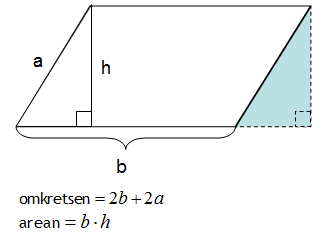
När man ska beräkna arean på en parallellogram, där motstående sidorna är parallella så använder man samma formel som för en vanlig rektangel. Om vi tittar på bilden nedan så ser vi att vi får en rektangel genom att flytta på parallellogrammens sidor, som vi har märkt ut som trianglar. Det viktiga är att du tar ut höjden i parallellogrammen genom att dra en normal från basen och upp.
En parallellogram har sidorna 37,3 mm och 12,5 mm och höjden 10,1 mm (höjden är vinkelrät mot den längre sidan). Bestäm parallellogrammens omkrets och area.
Vi börjar med att rita en figur och märker ut de måtten vi vet. Den längsta sidan var 37,3 mm och det var från den som höjden gick vinkelrätt ut ifrån. Den korta sidan var 12,5 mm.
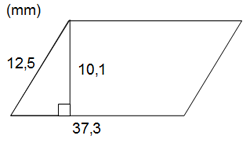
Notera att jag har skrivit mm inom parentes ovanför figuren – ett smidigt sätt att presentera att alla mått i figuren står i mm och så slipper man skriva till det efter varje siffra och riskera att figuren blir kladdig och rörig.
Omkretsen räknar vi ut genom att lägga ihop de fyra sidorna:
Arean är basen gånger höjden, där basen motsvarar 37,3 mm och höjden 10,1 mm.
Svar: Omkretsen är 99,6 mm och arean är 376,7 mm2.
Triangel
Arean för en triangel får vi ut genom att antingen se den som en halv rektangel eller en halv parallellogram. Detta ger oss att arean för en triangel är basen gånger höjden delat med 2.
Beräkna omkrets och area hos triangeln.
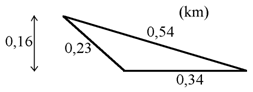
För omkretsen lägger vi ihop de tre sidornas olika längder:
Arean är basen gånger höjden delat med 2. 0,34 km motsvarar basen på triangeln och 0,16 km motsvarar höjden.
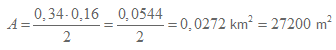
Svar: Triangelns omkrets är 1,11 km och arean är 27200 m2.
Parallelltrapets
Arean av ett parallelltrapets får vi genom att multiplicera höjden med summan av de parallella sidorna dividerade med 2. I bilden nedan ser vi hur vi kommer fram till detta. Parallelltrapetser har bara två parallella sidor. Om vi drar en diagonal delas det i två trianglar och då ser vi att arean för parallelltrapetsen är summan av de båda trianglarnas areor.
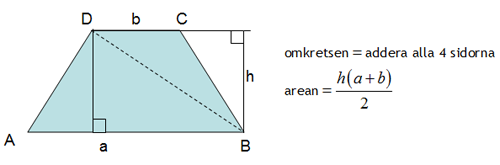
Beräkna parallelltrapetsens omkrets och area.
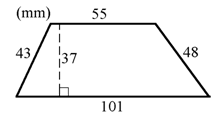
Vi börjar med att beräkna omkretsen som vi får fram genom att lägga ihop de 4 sidorna:
Formeln för arean säger att vi ska addera sidorna a och b och sedan gånga det talet med höjden och till sist dela med 2. Vi ser i figuren att a=101 mm och b=55 mm samt att höjden är 37 mm och kan då sätta in dessa tal i formeln och sedan räkna ut arean:
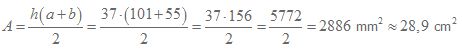
Svar: Omkretsen är 24,7 cm och arean är 28,9 cm2.
Kom ihåg att det gäller andra regler när man skriver om enheter som är i kvadrat! Skulle vi göra om 2886 mm till cm skulle vi, precis som vanligt, flytta kommatecknet ett steg åt vänster och på så sätt få 288,6 cm.
Men då enheterna är i kvadrat så blir ett steg istället lika med 2 steg.
3 m2 t.ex. är lika med 30 000 cm2. 3 m är ju 300 cm, och när det är kvadrerat så tar vi ett steg extra för varje steg, vilket resulterar i dubbelt antal nollor eller decimaler beroende på om man omvandlar till större eller mindre mått.
Romb
En romb är ett speciallfall av en parallellogram. Den ser likadan ut, men skillnaden är att alla sidorna i romben är lika långa. För att få fram omkretsen på en romb lägger du bara ihop alla fyra sidorna och eftersom de är lika långa kan vi säga att vi multiplicerar sidlängden med 4. Arean beräknas på samma sätt som hos en parallellogram.
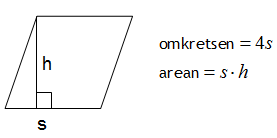
Beräkna rombens omkrets och area om denne har basen 17 cm och höjden 13 cm. (Höjden är vinkelrät mot basen).
Börja med att rita en figur och fyll därefter i med den information vi fått.
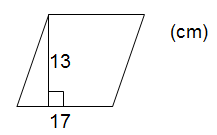
Omkretsen fås genom att multiplicera sidan (17) med 4:
Formeln för rombens area var basen (sidan) gånger höjden, 17 motsvarar basen och 13 motsvarar höjden:
Svar: Rombens omkrets är 68 cm och arean är 221 cm2.
Kvadratrötter
Kvadratroten är motsatsen till att kvadrera, alltså att ta ett tal upphöjt till 2. När man räknar ut kvadratroten på ett tal så blir svaret ett tal som multiplicerat med sig själv blir det tal man tog kvadratroten ur.
Beräkna .
Talen 5 och -5 är båda kvadratrötter ur 25 då båda 52 och (-5)2 är lika med 25.
Anledningen till att x även kan vara ett negativt tal när det gäller kvadratrötter är regeln som säger att minus · minus = plus.
Svar: x1=5 och x2=-5.
Räkneregler för kvadratrötter
Dessa regler gäller om a och b är positiva tal:
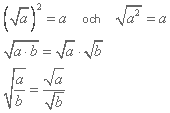
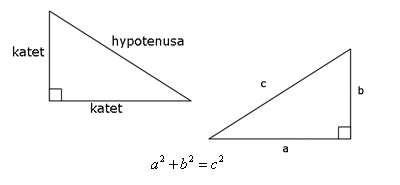
Pythagoras sats
Kan vi använda då vi vill ha reda på längden utav någon av sidorna i en rätvinklig triangel. De sidor som bildar den räta vinkeln i triangeln kallas för triangelns kateter medan den tredje sidan kallas för hypotenusa. I figuren här nedanför ser vi att om vi adderar de båda kateterna i kvadrat så får vi hypotenusans kvadrat.
Du har en rätvinklig triangel vars ena katet är 4 cm och den andra 5 cm. Hur lång är dess hypotenusa?
För att få en bättre överblick kan du rita upp triangeln.
Vi benämner hypotenusan med x. Pythagoras sats säger att:
Alltså:
eller bättre
Svar: Hypotenusan är 6,4 cm.
Du har en rätvinklig triangel. Dess ena katet är 3 cm och hypotenusan är 9 cm. Hur lång är den andra kateten?
Beteckna den andra kateten med x. Enligt pytagoras sats så är:
Lös ekvationen och du får svaret.
Svar: Den andra kateten är 8,5 cm.
Notera att i dessa två exempel har jag inte brytt mig om att anteckna att det även finns negativa lösningar på kvadratrötterna. Detta beror på att de båda exemplen handlar om att räkna ut en sträcka, och sträckorna kan ju som bekant inte vara negativa.
Cirklar och sektorer
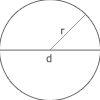Då vi ska räkna ut omkretsen och arean för en cirkel måste vi använda oss av konstanten , som uttalas ”pi”. Ett närmevärde med tre gällande siffror för är 3,14 och med fem gällande siffror blir det 3,1416. De flesta miniräknare har dock en särskild knapp föroch då föreslår jag att du använder den istället. Detta för att få ett så exakt svar som möjligt, och det är bättre att avrunda endast i slutet istället för att göra det redan från början. Då är risken att få fel svar större.
För att räkna ut omkretsen för en cirkel så tar vi diametern multiplicerat med. Diametern är det bredaste stället på cirkeln, man drar ett streck från cirkelns kantlinje, genom mittpunkten och sen fram till stället mittemot det man började. Diametern är samma sak som radien multiplicerat med 2.
Omkretsen för en cirkel är: eller
Arean av en cirkel får vi genom att multiplicera med radien i kvadrat. Radien är halva diametern, det vill säga avståndet från mittpunkten till cirkelns kant.
Arean av en cirkel är:
Hur stor är plåtbitens area (det färgade området) om hålets diameter är 30 mm?
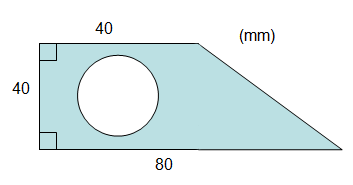
För att få fram plåtbitens area så ska vi ta plåtbitens hela area, alltså om det inte hade varit ett hål där, minus arean av cirkeln.
Börja med att räkna ut plåtbitens hela area. Vi delar in figuren i två delar, en kvadrat och en triangel och döper deras areor till A1 respektive A2.
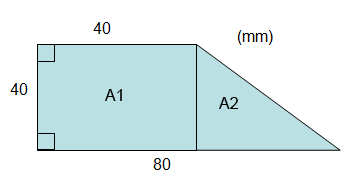
Vi vet att A1 är en kvadrat då figuren anger att både basen och höjden på fyrkanten är 40.
Triangeln har också basen 40 och höjden 40 då vi ser att den är lika hög som kvadraten. Likaså om triangelns och kvadratens baser tillsammans är 80 och kvadratens bas är 40 så måste triangelns bas utgöra de resterande 40.
Den sammanlagda arean (A3) för plåtbiten utan hål är således:
Nästa steg blir att räkna ut cirkelns area. Vi vet att diametern var 30 mm, och därför vet vi också att radien på den är 15 mm (r=30/2), vilket är det enda vi behöver för uträkningen.
Det inringade a:et betyder att jag har sparat det egentliga talet med en massa decimaler i grafräknarens minne på bokstaven A.
Plåtbitens area, det färgade området blir alltså:
Där det inringade a:et anger att jag har räknat ut svaret med det oavrundade talet.
Svar: Plåtbitens area är 1693 mm2.
Cirkelsektorer
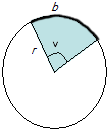En cirkelsektor begränsas av två radier och en cirkelbåge. I cirkeln till höger har vi blåmarkerat cirkelsektorn som har vinkeln v. Andelen av vinkeln v på hela varvet är v/360°.
Cirkelbågens längd är alltså v/360° av cirkelns omkrets. Då vi dividerar vinkeln v med det totala så får vi fram andelen av hela omkretsen. Om vi vill veta hur stor den andelen är måste vi multiplicera andelen med den totala omkretsen.
Längden på en cirkelbåge är:
Cirkelsektorns area får vi fram på samma sätt, fast vi multiplicerar andelen med cirkelns totala area istället.
Area för cirkelsektor är:
En cirkelsektor har radien 1 cm och vinkeln 60 grader. Beräkna dess omkrets och area.
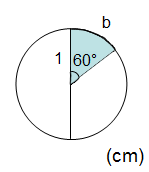Vi börjar med att rita en cirkel med cirkelbågen i sig. Den behöver inte ritas korrekt, det är bara för att uppgiften ska vara enklare att överblicka.
Omkretsen räknas ut genom att vi lägger ihop längden av de tre sidorna som utgör cirkelbågen, nämligen de två raka och sedan den böjda sidan. Uppgiften säger att radien är 1 cm, vilket innebär att vi redan fått veta längden på de båda raka sidorna och behöver nu alltså bara beräkna cirkelbågens längd för att kunna få fram cirkelsektorns omkrets.
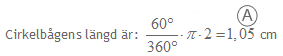
2:an är diametern som vi får fram genom att dubbla radien som ju var 1 cm.
Svaret innehåller egentligen en faslig massa decimaler, men som ni ser så har jag avrundat det och satt bokstaven A efter talet vilket betyder att jag har sparat hela talet i grafräknarens minne på bokstaven A, (se grafräknarsektionen), så att jag kan använda det senare.
Nu vet vi alla sidorna på cirkelsektorn och kan då räkna ut omkretsen:
(A visar att jag räknat ut omkretsen med det oavrundade talet.)
För arean så vet vi redan de tal som behövs; vinkeln v och radien r.
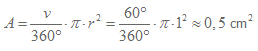
Svar: Cirkelsektorns omkrets är 3 cm och arean är 0,5 cm2.