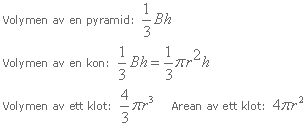Matte 1 - Geometri
Volym
Volym och begränsningsarea av rätblock, prismor och cylindrar
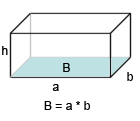
För att få ram volymen av ett rätblock multiplicerar vi bottenarean B med höjden. Man kan även säga att längden gånger bredden gånger höjden. Samma formel gäller även för prismor.
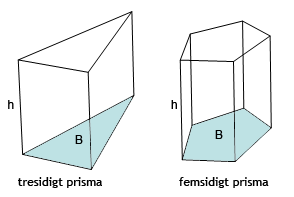
Var dock uppmärksam på att en tresidigt prisma t.ex. har en triangel som botten och du måste således använda formeln för en triangels area då du beräknar B. Likaså måste du uppmärksamma att en femsidigt prismas bottenarea består av både en rektangel och en triangel vilket gör att du måste kombinera areaberäkningsmetoderna för denna.
Begränsningsytorna är de ytor som formar kropparna. I en tresidig prisma t.ex. så är det två trianglar tillsammans med ett antal rektanglar som utgör begränsningarna i formen, medan ett rätblock enbart har rektanglar som begränsningar.
Mantelyta är den yta som är välvd i exempelvis en cylinder eller en kon.
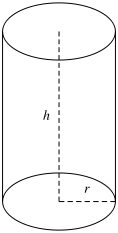Då vi beräknar en cylinders volym får vi dock tänka på en sak; dess bottenarea skiljer sig. Här kan man inte ta längden multiplicerat med bredden, utan botten är cirkelformad. Alltså får vi ta formeln för hur man räknar ut en cirkels area och sedan multiplicera den med höjden på cylindern.
Om vi ska räkna ut cylinderns mantelyta (den välvda ytan på cylindern) så multiplicerar vi basytans omkrets med höjden. Det är lättare att förstå om vi vecklar ut cylindern så att den blir till en rektangel istället. Längden på rektangeln är den ursprungliga omkretsen av cirkeln.
Kubikrötter
Om en kub ska ha volymen 27cm3 så måste kubens sidor vara 3 cm då 33 är 27. Detta innebär att talet 3 är kubikroten ur 27. Då man ska räkna ut kubikroten krävs det oftast en miniräknare. Då är det den här symbolen man ska leta efter:
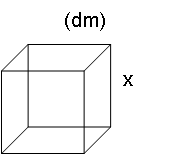En låda som är kubformad rymmer 120 dm3 vatten. Hur långa är dess sidor?
Börja med att rita upp en kub. I en kub är alla sidorna lika långa.
Antag: Sidan är x cm.
För att räkna ut kubens volym tar man ju sidan &middaot; sidan · sidan, alltså:
För att lösa ut x måste vi ta kubikroten ur 120:
Svar: Kubens sidor är 4,9 dm.
Volym och begränsningsarea av pyramider, koner och klot
Volymen för de olika figurerna här nedan får vi genom att räkna ut deras bottenarea, multiplicera den med höjden och sedan dividera med tre.
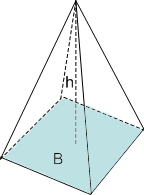
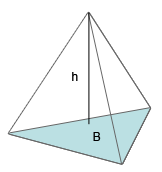
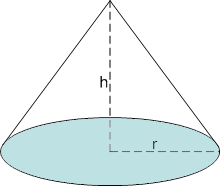
Längst till vänster syns en fyrsidig pyramid, i mitten en tresidig pyramid och längst till höger en kon.
Bilden under de tre övre bilderna visar ett klot med radien och diametern utmärkta. Arean av ett klot innebär dess mantelarea, alltså ytan runt klotet.
