Matte 1 - Grunder
Potenser
Potenser
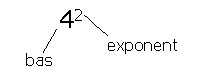
42 = 16 Detta kanske du känner igen från tidigare? Det betyder att du ska ta 4 * 4 = 16 En potens består av en bas och en exponent. De tal man multiplicerar med varandra kallas faktorer, i detta fall är det fyrorna. Basen anger den faktor som ska multipliceras medan exponenten talar om hur många faktorer som ska ingå i produkten. Produkten är resultatet av faktorerna. I detta fall så ska det finnas två stycken faktorer.
![]()
Skriv som en potens
a) b) c)
a)
Här ser vi tre stycken faktorer, alla har värdet 4. Vi kan då skriva 4 upphöjt till 3.
b)
Antalet faktorer i detta tal är 5 stycken, alltså 6 (faktorn) upphöjt till 5 (multiplicerat med sig själv 5 gånger).
c)
Det är ingen skillnad för decimaltal. Vi ser två faktorer därmed kan vi skriva 0,3 upphöjt till 2.
Svar: a) 43 b) 65 c) 0,32
Bestäm värdet utan att använda miniräknare
a) b) c) d)
a)
Enligt räknereglerna så går potenser före multiplikation när man bestämmer räkneordningen. Börja alltså med att räkna ut 52. Tvåan säger att det ska vara 2 faktorer med värdet 5 vilket blir 5 · 5 = 25. Nu när vi beräknat potensen kan vi multiplicera den med 4 och då får vi 100.
b)
Potenser går även före räknesätten addition och subtraktion. Vi räknar alltså ut potenserna var för sig och sedan kan vi utföra subtraktionen. 62 säger att vi ska mulitplicera 6:an med sig själv en gång (2 faktorer = 2 sexor). 6 · 6 = 36.
33 säger att vi ska ha tre faktorer som vardera har värdet 3. 3 · 3 · 3 = 27.
Sedan kan vi beräkna 36-27 som blir 9.
c)
Precis som i b-uppgiften beräknar vi först potenserna och sedan additionen. 32 blir 3 · 3 = 9 och 23 blir 2 · 2 · 2 = 8.
d)
Svar: a) 100 b) 9 c) 17 d) 1
Bestäm värdet på exponenten n så följande samband stämmer
a) b) c)
a) Multiplicera tvåan med sig själv så många gånger som behövs för att du ska få produkten 16.
Vi ser att det krävs 4 faktorer för att uppnå 16. Därmed är n=4.
b) Upprepa samma metod som a-uppgiften. Antalet treor som krävs motsvarar n.
n=4
c) Upprepa samma metod som a- och b-uppgiften. Antalet femmor som krävs för att uppnå 15 625 motsvarar n.
n=6
Svar: a) n=4 b) n=4 c) n=6
Multiplicering av potenser
Då två potenser med samma bas multipliceras med varandra så kan man lägga ihop exponenterna enligt följande regel:
![]()
Skriv som en potens
a) b)
a)
Dessa två potenser har samma baser, alltså kan vi använda regeln ovan som säger att man kan addera de båda exponenterna.
b)
Samma sak som i a-uppgiften fungerar också här då båda potenserna har basen 5. Vi kan se den ensamma femman som en potens också eftersom 51 = 5.
Svar: a) b)
Division av potenser
Om man dividerar två potenser med samma bas med varandra så subtraherar man exponenten i täljaren med exponenten i nämnaren enligt följande formel:
![]()
Skriv som en potens och beräkna värdet
a) b)
a)
Båda potenserna har samma baser, vi kan alltså tillämpa regeln ovan som säger att vi kan ta täljarens exponent minus nämnarens exponent och få en ny potens. därefter räknar vi ut värdet på den.
b)
Samma sak gäller här som i a-uppgiften. Vi får bara vara uppmärksamma på att det är ett negativt tal i exponenten hos nämnaren. Minus och minus blir plus istället.
Svar: a) b)
Upprepad potensbildning
Om du tar ett potenstal upphöjt till något så kan du multiplicera exponenterna med varandra och få en ny potens:
![]()
a) b) c)
a)
Enligt regeln ovan så kan vi multiplicera exponenten i potensen 102 med det tal som potensen i sin tur är upphöjt till.
b)
c)
Här är potensen 203 upphöjd till -3, kom ihåg det när du multiplicerar talen för du ska då få ett negativt tal som ny exponent.
Svar: a) b) c)
Olika baser
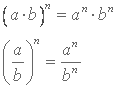
Beräkna .
Potenser går före multiplikation så vi börjar med att beräkna .
Enligt regeln ovan så är:
Fortsätt med att beräkna potenserna och utför sedan multiplikationen:
Svar:
Beräkna .
Potenser går före multiplikation så vi börjar med att få bort exponenten som berör hela parentsen.
Enligt regeln ovan så är:
Fortsätt med att beräkna potenserna och utför sedan multiplikationen:
Svar: 250 000
Potenser med negativ exponent och exponenten noll
Första regeln vi ska titta på är:
för alla värden på a förutom då
Som exempel kan vi ta talet
Om vi räknar ut så ser vi att kvoten blir 1.
Alltså måste också vara lika med 1.
Nästa regel är:
för alla värden på a förutom då
För att förstå denna regel så tittar vi på vad ett tal med negativ exponent egentligen innebär.
Om vi istället skriver ut vad uttrycken betyder:
Alltså är
Andra talexempel är:
a) Beräkna och skriv sedan som bråktal
b) Beräkna
a) När vi dividerar två potenser med samma bas så innebär det ju att vi tar den första exponenten minus den andra exponenten.
Om vi nu tittar på regeln angående negativ exponent så ser vi att
b) Återigen är det division. Här är det viktigt att komma ihåg att två stycken minus blir plus.
Svar: a) b)
Potenser med rationell exponent
Om så är
a är talet som multipliceras med sig självt n antal gånger.
Detta kan vi se t.ex. när vi ska beräkna hur lång sidan på en kub är. En kub har ju lika långa sidor, vi benämner dem x. Vi vet att volymen på kuben är 27 cm3 och kubens volym beräknas genom
Hur ska vi få reda på x? Talet som uppfyller detta är ju ett tal som är då
Kubens sida är 3 cm.
kallas för kubikroten eller tredje roten ur 27.
Likadant blir t.ex. och här säger man femte roten ur osv.
Om man skriver så menar man
Beräkna utan räknare
a)
b)
c)
a)
Det är talet 3 som gånger sig självt tre gånger bildar talet 27 enligt detta bevis:
b)
c)