Matte 1 - Statistik
Tolka data
När man gör olika statistiska undersökningar så blir det att man samlar in en hel del information eller data. Exempel på en statistisk undersökning kan vara när man frågar människor på stan vilket politiskt parti de tänker rösta på. För att få en bra överblick av svaren så sammanställer man dem oftast i tabeller och/eller diagram.
Begreppet observation innebär det man observerar/vill undersöka t.ex. vi vill veta vilket politiskt parti folk tänker rösta på i nästa val. Om vi säger att man kan välja mellan 7 olika partier så finns det 7 s.k. observationsvärden.
Frekvenstabeller
När man har många observationer använder man sig ofta av frekvenstabeller för att sammanställa materialet. I en frekvenstabell kan vi lätt utläsa hur många gånger som respektive observationsvärde förekommer – alltså frekvensen.
Elin hade haft en idrottslektion i hur man paddlar kajak och passade även på att föra lite statistik över hur många gånger klasskamraterna välte. Hon fick fram följande:
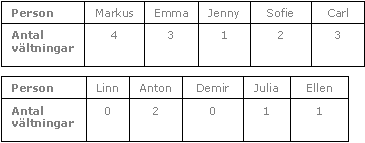
Sammanställ Elins observationer i en frekvenstabell.
I detta fall kan vi göra en sammanställning på hur många personer som välte hur många gånger. Vi börjar med att kolla hur många vältningar som gjordes. Från 0 upp till högsta antalet vältningar, vilket i detta fall var 4. Skriv upp en kolumn med rubriken Antal vältningar.
Därefter skriver vi till en kolumn till höger om första kolumnen. Denna kolumn ska ha rubriken Antal personer). Sedan är det bara att börja räkna. hur många personer välte 0 gånger? Jo, 2 stycken. fortsätt sedan så tills du gått igenom alla vältningar. Slutligen har du en färdig frekvenstabell som denna nedan:
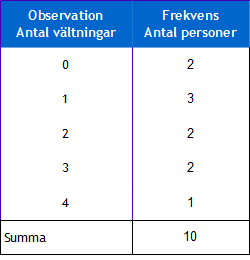
Ibland vill man även lägga till den relativa frekvensen i frekvenstabellen. Om vi skulle göra det med tabellen ovan så skulle vi lägga till en kolumn med rubriken “Relativ frekvens” och sedan beräkna procentsatsen för respektive observationsvärde. Detta gör vi genom att dela varje frekvens med totalen dvs. antalet personer för varje vältning delat med totala antalet personer (10). Resultatet skulle se ut såhär:
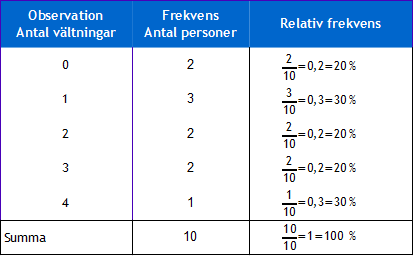
Svara på följande frågor m h a frekvenstabellen i förra exemplet.
a) Hur många av Elins klasskamrater välte mindre än 3 gånger?
b) Hur många procent av klasskamraterna var de som välte mindre än 3 gånger?
c) Elins idrottslärare försökte sig också på att paddla och kom undan med 2 vältningar. Hur många procent av deltagarna välte 2 gånger?
a) De observationsvärden som möter kravet “mindre än 3″ är de som säger att antalet vältningar var 0, 1 eller 2 stycken. Vi får helt enkelt lägga ihop antalet personer som antingen välte 0, 1 eller 2 gånger.
7 st av Elins klasskamrater välte mindre än 3 gånger.
b) Detta kan vi lösa på två sätt. Antingen lägger vi ihop procentsatserna vi ser under “relativ frekvens” för antalet vältningar eller så räknar vi ut den relativa frekvensen baserat på den nya siffran (7):
c) Från början var det 2 stycken personer som hade vält 2 gånger. Nu har observationsvärdet 2 vältningar fått tillskott av ytterligare en person. Det är alltså 3 stycken som har vält 2 gånger. Om vi ska beräkna den nya relativa frekvensen för detta observationsvärde så delar vi frekvensen (3) för observationsvärdet med totala antalet personer. Notera att det nu är totalt 11 personer som har deltagit, inte 10.
Svar: a) 7 personer välte färre än 3 gånger. b) De motsvarar 70% av deltagarna c) 27% av deltagarna välte 2 gånger.
Olika typer av data
Ordet variabel används även inom statistiken och med det menar man att ett värde varierar mellan olika individer. Du vill t.ex. undersöka hur långa personerna är i en klass. Det är ju aldrig så att alla individer är lika långa, därmed varierar längden mellan olika personer. Det du undersöker, längden, är en variabel.
När man gör en statistisk undersökning finns det två olika typer av variabler:
- Kvalitativa variabler
- Kvantitativa variabler
KVALITATIVA VARIABLER
Detta är variabler som man inte kan räkna med, de består inte av tal (är inte numeriska).
Exempel: kön, vilket typ av husdjur individer äger, vilken typ av bil folk kör osv.
KVANTITATIVA VARIABLER
Dessa variabler är tal man kan räkna med, variablerna är numeriska.
Exempel: antal barn, antal bilar, temperatur, blodvärde osv.
Diagram
Ofta är det lättare att överskåda den data man samlat in genom att man presenterar dem med olika typer av diagram. I diagrammen kan man lätt se hur data fördelas eller hur det förändras.
När man ska presentera statistik baserat på kvalitativa data brukar man oftast använda sig av cirkel- eller stapeldiagram:
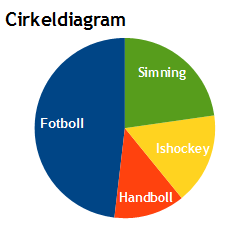
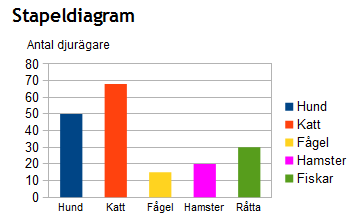
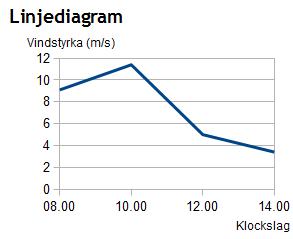
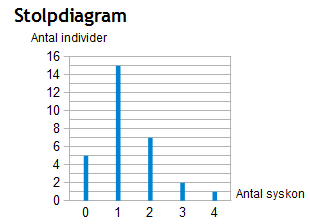
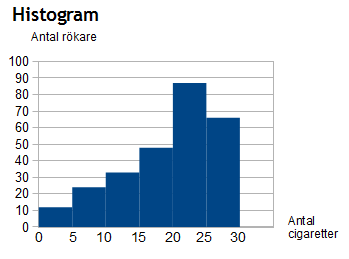
Om det istället gäller kvantitativa data beskriver man det hellre med linjediagram, stolpdiagram eller histogram.