Matte 2 - Algebra och ickelinjära modeller
Exponentialfunktioner
Innan du börjar läsa detta kan det vara bra att friska upp minnet kring potenser.
En potens består av en bas och en exponent.
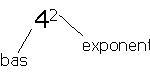
Potensregler
Här presenteras de potenslagar som kan komma till nytta i efterföljande avsnitt.
| Potensregel | Exempel |
|---|---|
Potensekvationer
Ett exempel på en potensekvation är .
Denna ekvation visar oss med hur mycket datorn sjunker i värde för varje år som går. Genom att vi vet hur många sänkningar som görs (3 stycken) och vad ursprungsvärdet och slutvärdet är kan vi beräkna hur mycket datorn sjunker i värde för varje år.
En potensekvation har utseendet där det obekanta talet är en bas.
Potensekvationen har lösningen
M h a denna regel kan vi beräkna hur mycket datorns värde sjunker varje år.
Alltså för varje år minskar datorns värde till 80% mot tidigare år, dvs. en årlig sänkning på 20%.
En stads befolkning ökade på 18 år från 20 200 till 38 400. Beräkna den genomsnittliga årliga procentuella ökningen. Återigen betecknar vi ändringsfaktorn som x och vi får då följande ekvation:
Ändringsfaktorn i detta fall blir talet 1,04 vilket innebär en ökning på 4 %.
Lös potensekvationerna
a) b) c)
d)
a) eller
b) eller
c) eller
d) eller
Exponentialfunktioner och exponentialekvationer
Ett exempel på en exponentialfunktionär
Funktionen är konstruerad så att du alltid får ett visst värde på y då du stoppar in ett värde för x. Här betecknar y priset på en dator och funktionen visar hur mycket en dator är värd från det att man precis har köpt den och hur den sedan tappar i värde allteftersom åren går.
10 000 utgör startsumman, alltså vad datorn kostade som ny. Vi ser att man multiplicerar 10 000 med 0,8 vilket innebär att för varje år som går så sjunker datorns värde med 20%. x betecknar antalet år som har gått.
Om vi vill veta hur mycket datorn är värd använder vi alltså denna funktion. Om vi vill veta värdet efter 1 år så ersätter vi x med 1:
Datorn är alltså värd 8 000 kr efter 1 år.
Om vi vill veta hur mycket datorn är värd om 2 år skriver vi:
Notera att 8 000 är detsamma som , beräkningen är detsamma som:
Med hänvisning till potenslagen , som säger att man kan lägga ihop exponenterna för två likadana baser som multipliceras med varandra, så ser vi att vi kan slå ihop 0,8:orna till 0,82. Varje 0,8 är detsamma som 0,81.
Om vi istället vill veta hur många år det har gått när datorn är värd 2 000 kr så ersätter vi y med 2 000 (y motsvarade ju värdet på datorn) och då har vi bildat en exponentialekvation:
I en exponentialekvation är det obekanta talet en exponent.
Hur löser man nu denna ekvation?
Det finns 2 typer av exponentialekvationer.
- Enkla exponentialekvationer
- De man löser med hjälp av logaritmer
De som man löser med hjälp av logaritmer går vi igenom lite senare på sidan.
De enkla exponentialekvationerna kan man antingen lösa genom att testa sig fram eller via grafisk lösning.
Ta t.ex.
Om vi testar oss fram:
så ser vi att det krävs att man multiplicerar 3 med sig själv en gång, dvs. det krävs 2 stycken 3:or(faktorer) för att få produkten 9. Alltså x = 2:
Ett annat exempel där vi kan testa oss fram är :
Vi ser att det krävs 3 stycken 4:or (faktorer) för att få produkten 64, alltså är x = 3.
Man kan även använda sig av potenslagarna för att beräkna vissa exponentialekvationer, t.ex. .
Ekvationen kan tyckas klurig, men om man kommer ihåg potensregeln så kan vi konstatera att talet 4,32 måste vara upphöjt med 0.
Om vi återgår till den exponentialekvation vi bildade här ovan, . Som ni märker blir denna exponentialekvation svår att lösa genom att prova sig fram. Vi kan komma så långt så att vi får variabeln x ensam på en sida, men sen är det stopp.
Här får vi istället ta till en grafisk lösning, dvs. vi plockar fram vår grafräknare och där vi matar in vänsterled respektive högerled som varsin funktion:
och
Därefter trycker vi på GRAPH:
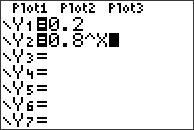
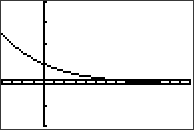
Lösningen på ekvationen hittar vi i den punkt där de båda graferna skär varandra. Vänsterled hade värdet 0,2 och därför blir det bara en rak linje som passerar genom y-axeln vid just 0,2. Grafen för antar olika y-värden beroende på vad dess x-värde är. För att få reda på vad x har för värde i denna ekvation så måste vi titta på x-värdet i den punkt där grafen har värdet 0,2 dvs. där linjen y=0,2 skär -grafen.
För att hitta punkten där de båda graferna korsar varandra ska vi utnyttja funktionen “intersect”. Tryck på knappen CALC (2nd+TRACE) och välj alternativ nummer 5:intersect (=”korsa”). Grafräknaren ber dig nu att markera var kurvorna korsar varandra. Först följer man den ena kurvan, använd piltangenterna för att flytta markören närmare korsningsstället, sedan samma sak för den andra kurvan. Slutligen ombeds man att gissa var de båda kurvorna korsar varandra och grafräknaren räknar sedan ut var punkten befinner sig. Punkterna väljs med hjälp av ENTER-knappen.
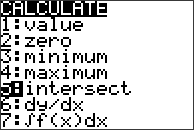
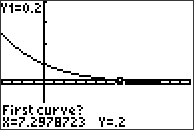
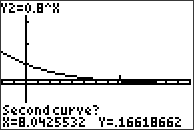
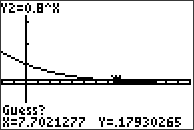
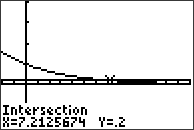
Vi ser att lösningen är . Svaret blir alltså att datorn är lite äldre än 7 år när den har nått värdet 2 000 kr.