Matte 2 - Algebra och ickelinjära modeller
Logaritmer
Exponentialekvationer och logaritmer
Vi har sett att det ofta är så att man inte lyckas få ett exakt värde på x i en exponentialekvation. Om vi fokuserar på de exponentialekvationer som ser ut enligt följande:
…så finns det en metod för att kunna skriva en exakt lösning.
1. Först har vi det s.k. enkla fallet, dvs. de fall där både vänsterled och högerled skrivs med basen 10.
2. Sen har vi de något mer komplicerade fallen där baserna mellan höger- och vänsterled skiljer sig åt t.ex. exopnentialekvationen .
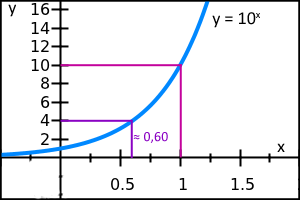
Vi kan ju lösa den grafiskt genom att rita upp funktionen och sedan läsa av x-värdet i den punkt där y = 4, men vi kommer bara få ett ungefärligt svar (0,602059991…) med oändligt massa decimaler.
Om vi vill ange ett exakt värde på exponenten x som ger att så är detta 10-logaritmen för 4. Man kan även skriva det som
I denna graf kan vi alltså se vilket tal (0,6) vi måste höja upp 10 med för att få t.ex. 4. Vi kallar talet 0,6 för eftersom det är det talet som vi upphöjer 10 med för att få 4.
Vi kan alltså lösa en exponentialekvation:
- grafiskt, genom att läsa av punkten i grafen; eller
- algebraiskt, dvs exakt genom att ange 10-logaritmen
Grafräknaren kan ge noggrannare närmevärden till 10-logaritmer, knappen brukar oftast ha skrivet “log” på sig. Testa gärna genom att skriva “log” och sedan 4 och klicka enter så ser ni att ni får 0,602…osv.
Baserat på detta kan vi konstatera följande:
Om så är x detsamma som i de fall där y är ett positivt tal.
Notera att:
- sägs vara skrivet i potensform; medan
- sägs vara skrivet i logaritmform
Det är viktigt att kunna växla mellan dessa.
Skriv som logaritmform
a) b) c)
a)
Vi vet att det tal som vi måste höja upp 10 med för att få 10 000 är 4:an motsvarar x:et och resultatet av upphöjningen är 10 000. 4:an kallas alltså lg 10 000.
b)
Här är det nollan som vi höjer upp med för att få 1. lg 1 är benämningen på nollan:
c)
Här används -5 för att få 0,000 01. -5 benämns alltså
Svar: a) b) c)
Skriv som potensform
a) b) c)
a)
b)
c)
Svar: a) b) c)
Logaritmlagar
Logaritmen för en produkt:
Logaritmen för en kvot:
Logaritmen för en potens:
Lös ekvationen med hjälp av logaritmlagarna
a) b)
a) Om vi tittar på logaritmlagen för en produkt så ser vi att när man lägger samma två olika logaritmer så är det detsamma som logaritmen för produkten av de båda talen som logaritmeras, dvs. talen som är logaritmerade multipliceras med varandra innan logaritmeringen utförs.
Vi har x på vänster sida och talen på höger sida om likhetstecknet. och slås samman till en logaritm där talen multipliceras med varandra. När vi vet att är detsamma som så måste ju x motsvara 8.
b) I detta tal tittar vi istället på logaritmen för en kvot. Vi ser där att en logaritm minus en annan logaritm också kan skrivas som en logaritm där de båda logaritmerade talen istället ställs upp som en division. Talet som man drar ifrån med, i detta fall femman, placeras i nämnaren, medan talet som subtraheras, dvs. åttan, placeras i täljaren.
Svar: a) b)
Logaritmer med olika baser
Överst på sidan så gick vi igenom 10-logaritmer, alltså lösningen för en okänd exponent i en potens med basen 10. Ett exempel på detta är där exponenten x benämns “10-logaritmen för 4″ och skrivs som eller
Men om nu basen skulle vara 5 istället?
Jo, då säger vi helt enkelt att exponenten x är lika med “5-logaritmen för 4″ och detta skrivs som
Om basen är 9, så är exponenten x lika med “9-logaritmen för 4″, vilket skrivs som
Vi kan alltså konstatera att:
De logaritmlagar vi har tittat på ovan gäller även för de andra baserna.