Matte 2 - Algebra och linjära modeller

Linjär anpassning

Skriv ut

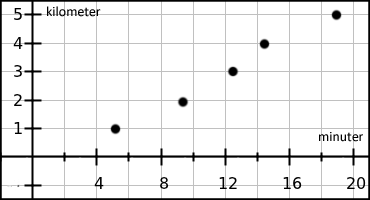Alfons sticker ut på en löprunda på 5 km. Då Alfons kompis Sammi är matematikintresserad så kollar han hur många minuter det har gått för varje kilometer Alfons har sprungit. Sammi markerar sedan mätvärdena i ett koordinatsystem där vi ser att det tog dryga 5 minuter för Alfons att springa första kilometern och nästan 1 minut snabbare andra kilometern osv. Sammi vill nu beskriva hur långt (y kilometer) Alfons har sprungit efter en viss tid (x minuter) och han vill beskriva detta med en linjär modell, dvs. man tänker sig att Alfons har samma hastighet hela tiden. Den linjära modellen har utseendet y = kx + m.
Nu var det ju så att Alfons inte riktigt höll samma hastighet hela tiden.

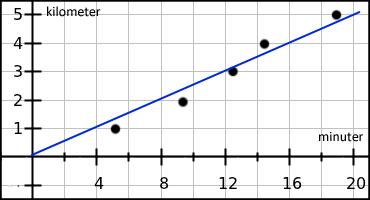För att få en så rättvis bild som möjligt så ritar vi en rät linje som i allra möjligaste mån ligger lika nära alla 5 punkterna i diagrammet. Det är denna linjes ekvation som kommer att agera modell för hur sträckan varierar med tiden.
Vi beräknar först riktningskoefficienten k med hjälp av linjens koordinater (0, 0) och (16, 4):


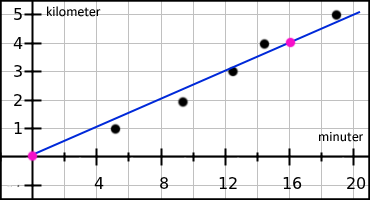
m är detsamma som y-värdet där linjen korsar dvs. där x = 0. Eftersom denna linje startar i origo (0, 0) så är m = 0. Linjens ekvation är således:
y = 0,25x
Med hjälp av denna kan vi snabbt se t.ex. att när Alfons har sprungit i 1 minut (x = 1) så har han hunnit 250 meter (0,25 km).

Observera dock att vi ritade upp denna linje enbart med hjälp av vårt ögonmått! Vi ritade den så att vi tyckte att det såg ut som om den låg så nära som möjligt alla 5 punkterna samtidigt. Om var och en av er skulle rita en egen linje skulle vi sannolikt få många olika linjer med olika ekvationer. Hur får vi då fram den bästa linjen? Den som mest stämmer överens med de värden vi har fått? Jo vi kan använda oss av minsta kvadratmetoden.

Minsta kvadratmetoden

Minsta kvadratmetoden går ut på att man tittar på avståndet mellan en dragen linje och de olika mätpunkterna. Hur långt är det mellan linjen och punkt 1 (d₁), hur långt är det mellan linjen och punkt 2 (d₂) osv.
Dessa avstånd kvadrerar vi (avstånd ²) och lägger sedan ihop dem. Den linje som får lägst summa när man lägger ihop alla kvadrerade avstånd är den bästa linjen.

Linje 1:
Linje 2:
Linje 3:

Av de tre olika linjerna man ritat upp så är det linje 2 som är bäst.
Våra grafräknare fixar detta galant och fort går det! Man säger att man har gjort en linjär regression.

Gillade du denna sida? Hjälp andra att hitta den!

Genom att trycka på länkarna här över så sprider du ordet om Matteguiden och hjälper oss att växa. På så sätt kan vi fortsätta att hjälpa besökare som behöver hjälp med matten.