Matte 2 - Algebra och linjära modeller
Linjära ekvationssystem
Här nedan ser vi ett så kallat ekvationssystem. Det är två ekvationer och “klammern” är till för att visa att y har samma värde.
Om man tittar på ekvationerna var för sig så ser man att de kan ha oändligt många lösningar, exempel på dessa ser du nedan.
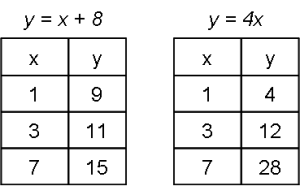
Grejen med ekvationssystem är att man bestämmer de ingående ekvationernas gemensamma lösning. Alltså det finns ett visst värde på x som funkar som lösning för båda ekvationerna och båda ekvationerna har då samma y-värde. Detta illustreras tydligt i en graf som vi ska kika på nedan.
Vi kan lösa ekvationssystemen på två sätt; algebraiskt eller grafiskt. Båda sätten är relativt enkla.
Grafisk lösning
En grafisk lösning av ekvationssystem bygger helt enkelt på att man bestämmer skärningspunkten mellan linjerna med de två ekvationerna. Det är koordinaterna i skärningspunkten som utgör lösningen till ekvationssystemet.
(Detta exempel är hämtat ur Gleerups Delta Matematik kurs A och B.)
Lös ekvationssystemet grafiskt.
Rita upp de båda linjerna antingen på ett papper eller i miniräknaren.
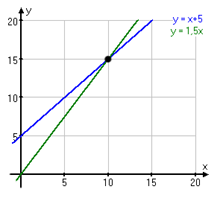
Linjerna har ekvationerna respektive . Skärningspunkten mellan linjerna har koordinaterna x=10 och y=15, vilket innebär att lösningen till systemet är x=10 och y=15.
Svar: x=10 och y=15.
Algebraisk lösning
Detta sätt att lösa ekvationssystem kan ibland vara att föredra eftersom det ger ett exakt värde på lösningen och kan även vara enklare att genomföra.
Lös ekvationsystemet
Sätt båda y-värdena lika med varandra.
För att få fram y så sätter vi in bara in x-värdet i en utav ekvationerna.
Insättning ger:
Svar: Lösningen är
Algebraisk lösning – Substitutionsmetoden
Denna metod bygger på att vi löser ut en variabel, antingen x eller y, i den ena ekvationen och ersätter (substituerar) den variabeln i den andra ekvationen med det uttryck man får. Därefter kan vi lösa ekvationen.
Om vi t.ex. löst ut x så måste vi sedan sätta in x-värdet i en av ekvationerna för att kunna räkna ut y-värdet.
Lös ekvationssytemet
Vi löser ut y i den första ekvationen…
…och ersätter y i den andra ekvationen med det uttryck vi fick fram:
Nu när vi vet vad x har för värde så kan vi också beräkna värdet på y:
Svar: Lösningen är
Algebraisk lösning – Additionsmetoden
Additionsmetoden är ett alternativ till substitutionsmetoden och är lämplig att använda när man inte kan lösa ut en variabel på ett enkelt sätt. Additionsmetoden bygger på att vi:
- ser till att en av variablerna (y eller x) i båda ekvationerna har ett tal framför sig (koefficient) som i ena ekvationen är motsatt tal till det i den andra ekvationen t.ex. -6y och +6y eller -2x och +2x. Detta ordnas genom att man multiplicerar den ena eller båda ekvationerna med lämpliga tal så att man får detta utseende (se exempel nedan).
- adderar därefter de båda vänsterleden och de båda högerleden med varandra och sätter dem sedan lika med varandra. Vi har då skapat en ekvation med en variabel som vi kan lösa.
- Lösningen på ekvationen t.ex. om vi fått ut y-värdet, sätter vi in i en av ekvationerna för att beräkna x-värdet.
Lös ekvationssytemet
Här ser vi att vi kan skippa första steget med multiplikation eftersom vi redan har en variabel som i en av ekvationerna är den motsatta mot den i den andra ekvationen, nämligen +y och -y. Vi kan genast gå över till att addera de båda ekvationerna och ser då att y-termerna försvinner och därmed har vi skapat en ekvation där vi kan lösa ut x.
För att sedan få fram y-värdet så sätter vi in x-värdet i en utav ekvationerna:
Svar: Lösningen är
Lös ekvationssytemet
Här krävs det att vi utför multiplikation innan vi kan addera vänster- respektive högerleden. Vi multiplicerar den första ekvationen med 3 och den andra med -2 för att koefficienterna hos x-termerna ska bli motsatta tal och därmed försvinna när vi lägger ihop vänsterleden och högerleden. Att vi väljer x är enbart slumpen, man skulle lika gärna kunna utföra en multiplikation som gör att y försvinner vid addering.
Vi adderar vänsterleden respektive högerleden och löser ekvationen.
Sätt in y=1 i en av ekvationerna för att ta reda på x-värdet:
Svar:
Ekvationssystem med tre olika variabler
Ett exempel på en ekvation med tre variabler är , om man har ett ekvationssystem med tre sådana ekvationer så kan man i de flesta fall beräkna alla tre variablerna.
Första steget är att eliminera en av variablerna m h a substitutions- eller additionsmetoden så att vi får ett ekvationssystem med två variabler.
Om vi tittar på ekvationerna så ser vi att vi inte på något enkelt sätt kan lösa ut en av variablerna och därför är det lämpligare att använda additionsmetoden.
Börja med att kika på ekvation nummer 1 och 2. Här är det så bra ordnat att vi har +4y och -4y och därmed kan vi direkt gå vidare till att addera vänsterleden med varandra och högerleden med varandra:
Därefter tittar vi på ekvation nummer 2 och 3 där vi också vill utesluta y. Här krävs det dock att vi multiplicerar ekvation nummer 2 med 2 för att kunna få motsatta variabeln -8y:
Nu kan vi addera vänsterleden respektive högerleden i ekvation nummer 2 och 3:
Med de två nya ekvationerna kan vi nu bilda ett nytt ekvationssystem där vi kan lösa ut variablerna som vanligt:
Eftersom vi har +8z i båda ekvationerna skulle vi kunna substituera en utav dem. Vi väljer första ekvationen där vi flyttar om termerna så vi får Uttrycket använder vi för att ersätta 8z i ekvationen :
Därefter är det bara att lösa ut x:
När vi vet att x = -1,5 kan vi sätta in det i en utav formlerna innehållande bara x och z för att få ut z-värdet:
Slutligen, vi kan nu ta reda på y-värdet genom att stoppa i värdena för x och z i en utav de ursprungliga tre ekvationerna:
25 januari 2015 @ 20:12
Värdelöst
29 juni 2015 @ 19:57
Detta förklarade vad jag inte kunde förstå i matteboken. Tackar!