Matte 2 - Geometri
Likformighet
Likformighet
Då två figurer är likformiga så har de precis samma form, men är olika stora. Det vi då kan utnyttja är att deras motsvarande vinklar är lika stora och därmed är sidorna proportionella.
Likformiga månghörningar har
- motsvarande vinklar lika stora
- lika förhållanden mellan motsvarande sidor
Observera att trianglar är ett undantag/specialfall vad gäller reglerna för likformighet. De behöver bara uppfylla ett av kraven, närmare bestämt om det råder likformighet mellan trianglar om två av deras motsvarande vinklar är lika.
Likformiga trianglar har två motsvarande vinklar som är lika.
Beräkna längder i likformiga figurer
Om man har 2 likformiga figurer där en sidan i den ena figuren är okänd så kan man utnyttja det faktum att det råder samma proportionalitet mellan sidorna i de båda figurerna.
T.ex. förhållandet mellan två figurers baser är detsamma som förhållandet mellan deras höjdmått.
Förhållandet skrivs t.ex. då som
Alltså, för likformighet krävs det att kvoten mellan figurernas baser är densamma som kvoten mellan deras höjder:
Om alla tal är kända utom t.ex. höjden i andra figuren så kan vi möblera om i uttrycket så vi får uttrycket:
…och därmed kan vi beräkna höjden i andra figuren.
Två figurer är likformiga om kvoten mellan motsvarande avstånd överallt är densamma. Kvoten är skalan mellan figurerna.
Om vi nu tittar på de två romberna där de båda baserna och den ena höjden har märkts ut. Höjden i första figuren är dock okänd, beräkna denna. Måtten är angivna i cm.
Enligt regeln ovan så får vi fram skalan mellan de båda figurerna genom att dividera de båda kända baserna.
Förhållandet mellan den lilla och stora romben är 1:, alltså den stora är gånger så stor som den lilla.
Vi kan då beräkna den okända höjden i den lilla figuren genom att dividera den stora rombens höjd med :
Svar: Höjden i den lilla romben är 4,8 cm.
Topptriangelsatsen och transversalsatsen
En transversal är en rät linje som skär två eller flera linjer. En parallelltransversal är en transversal som dessutom är parallell med en sida i en triangel.
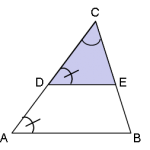
I och med detta så delar en parallelltransversal en triangel så att denna får en topptriangel. Denna topptriangeln är likformig med den stora triangeln.
Topptriangelsatsen
En topptriangel skapas av en parallelltransversal. Topptriangeln är likformig med hela triangeln.
Likformigheten mellan topptriangeln (CDE) och hela triangeln (ABC) bevisas genom att de båda trianglarna har två lika motsvarande vinklar. Vinkeln i deras vänstra hörn är lika stor då deras sida som utgår från det hörnet lutar lika mycket. Därtill delar de samma toppvinkel.
Med andra ord är t.ex. förhållandet mellan deras baser (AB och DE) detsamma som förhållandet mellan deras högra sidor t.ex. (CE och CB):
Transversalsatsen säger att en paralleltransversal delar två sidor i en triangel i samma förhållande. Detta innebär att förhållandet mellan sidan AD och DC är detsamma som förhållandet mellan BE och EC.
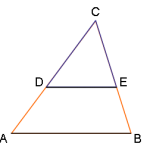
Topptriangelsatsen och transversalsatsen kan utnyttjas för att beräkna okända sidors längd. Vilken utav dem man använder beror på vilken information du får för att kunna lösa talet.
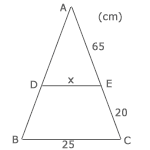Beräkna längden av DE i triangel ABC.
Om vi tittar på triangeln så ser vi att linjen DE är en parallelltransversal och därför är topptriangeln likformig med triangel ABC. Vi använder oss av topptriangelsatsen för att lösa detta problem eftersom figuren inte innehåller någon information om vilka mått som triangeln har på sin vänstra sida.
Det innebär att förhållandet mellan den stora triangelns bas och den lilla triangelns bas är lika stort som förhållandet mellan den stora triangelns sida och den lilla triangelns sida. Förhållandet får vi genom att dela den lilla triangelns mått med den stora triangelns mått eller tvärtom.
Antag: Sidan DE är x cm.
Svar: Linjen DE är 19 cm lång.
Kongruens
Då två figurer är likformiga och lika stora, dvs. kopior av varandra, så säger man att de är kongruenta.
Bisektrissatsen
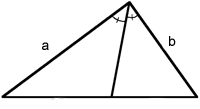En bisektris är en linje som dras rakt ut från ett hörn så att vinkeln i det hörnet delas i två lika stora vinklar. Då bisektrisen når motstående sida så delar bisektrisen den sidan i två sidor. Förhållandet mellan dessa sidor är detsamma som förhållandet mellan de två sidor (a och b) som går ut från hörnet bisektrisen delade mitt itu.
Om två sidor i en triangel har längderna a och b delar bisektrisen till vinkeln mellan dessa båda sidor och den tredje sidan i förhållandet a:b.
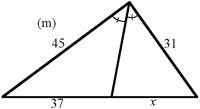Beräkna sträckan x.
Enligt bisektrissatsen så är förhållandet mellan sidan som är 45 m och sidan som är 31 m detsamma som förhållandet mellan 37 m och x m. 45 delat med 31 ska alltså få samma kvot som 37 delat med x. På så vis kan vi sätta upp en ekvation där vi kan lösa ut x:
Svar: x = 25 meter.
Areaskala och volymskala
Areaskalan förklaras under geometri i Matte A.
Volymskalan fungerar nästan på samma sätt som areaskalan, men här måste man ta skalan upphöjt till tre. Volymens enhet benämns ju som bekant i kubik-meter, -cm etc, alltså 3.
Längdsakala:
Areaskala:
Volymskala:
29 april 2013 @ 18:34
I exempel 2 förstår jag inte riktigt hur det blir 85x (och inte 65x) kan ni snälla och förklara, har lite problem med liknande uppgifter…
16 maj 2014 @ 12:31
En lite enklare metod:
Ställ upp —> x/25 = 65/85 (85 är hela summeringen av triangelns högra sida 65+20)
För att räkna ut x:
x = (25*65)/85 ≈ 19
Denna metod funkar på väldigt många liknande frågor. Testa på andra uppgifter (te.x. exempel 1 och 3). Underlättade för mig, iallafall