Matte 2 - Geometri
Vinklar
Repetition
Innan ni fortsätter att läsa rekommenderar vi att ni repeterar det som tas upp om vinklar i matte 1 ifall ni känner att ni behöver friska upp minnet.
Om inte, varsågoda att scrolla ner! 
Yttervinkelsatsen
Yttervinkelsatsen
Yttervinkeln är summan av de två motstående inre vinklarna.
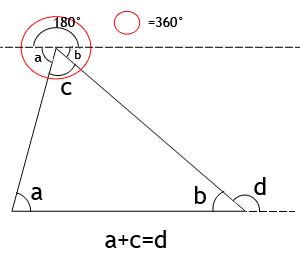
Detta kan vi bevisa: Tänk er en likadan röd ring som i det övre hörnet, fast placera den i det nedre högra hörnet istället. Utrymmet under linjen vid hörnet b blir 180°, och därmed vet vi att vinklarna b och d tillsammans är 180°. Vi vet också sedan innan att vinklarna b, c och a tillsammans är 180°. Då kan vi säga att vinklarna c och a tillsammans utgör summan på vinkeln d.
Medelpunktsvinklar och randvinklar
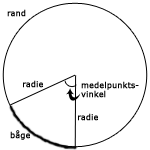Medelpunktsvinkeln är den vinkel som bildas då man drar två radier i en cirkel (en radie är en rät linje som går från cirkelns kant och in till mitten). Vinkeln står på två så kallade ben, alltså de båda radierna. Sträckan mellan dessa två punkter på cirkelns ytterkant kallas för båge.
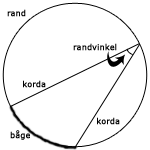En randvinkel bildas av att man förbinder en punkt på cirkelns rand med två andra punkter på randen. Detta görs med hjälp av två räta linjer s.k. kordor. Som ni ser står randvinkeln med sin två ben på en båge, precis som medelpunktsvinkeln.
Vad har vi för nytta av att kunna detta? Jo, ifall en medelpunktsvinkel och en randvinkel står på samma båge i en cirkel så finns det ett enkelt samband mellan vinklarnas storlek. Detta samband kallar vi för randvinkelsatsen.
En randvinkel i en cirkel är hälften så stor som den medelpunktsvinkel som står på samma båge.
Därtill kan vi lägga till dessa två regler:
Alla randvinklar som står på samma båge i en cirkel är lika stora.
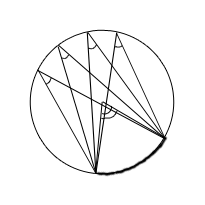
En randvinkel i en halvcirkel är rät, alltså 90 °.
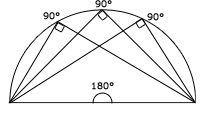Den första regeln menar att randvinklarna fortfarande är hälften av medelpunktsvinkeln oavsett var någonstans de befinner sig på randen så länge som de står på samma båge.
Den andra regeln är enkel att förstå, i en halv cirkel så är medelpunktsvinkeln 180 grader och randvinkeln är hälften utav det, alltså 90 grader.
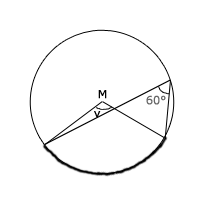Hur stor är vinkeln v i figuren? M är cirkelns medelpunkt.
Om vi tittar på bilder så ser vi att 60 gradersvinkeln är en randvinkel då den har två ben ståendes på en båge och de möts och bildar en punkt på randen. Vinkeln v är en medelpunktsvinkel, i och med att de båda vinklarna står på samma båge kan vi använda oss utav randvinkelsatsen.
Det ger oss:
(^ = vinkel)
Svar: Vinkeln M = 120°.
6 november 2013 @ 21:42
.) Vinkeln A är 10 grader mindre än vinkeln B, och vinkeln v är 60 grader större än vinkeln B. Beräkna v.