Matte 2 - Statistik
Spridningsmått
Spridningsmått
Om vi har fört statistik på, låt säga, hur väl två klasser har lyckats på samma prov så har vi siffror på hur många elever i varje klass som hade ett visst antal poäng.

Om man tar beräknar differensen (skillnaden) mellan den största och minsta poängen klasserna för sig så får man fram variationsbredden för respektive klass.
Klass 7a fick variationsbredden:
Klass 7b fick variationsbredden:
Detta innebär att spridningen av poängen är större i b-klassen än i a-klassen.
Ur statistisk synpunkt så är det bättre ju mindre spridningen är eftersom det innebär att alla värden man har observerat samlar sig närmare runt ett specifikt värde. På så vis får man starkare bevis för att just den specifika situationen/värdet tycks gälla.
Det finns dock en nackdel med att använda variationsbredden för att se hur pass spritt ett material är. Av alla värden man har samlat in så tar den bara hänsyn till två av dem, det största och det minsta. Man får inte alls veta hur resterande värden förhåller sig till varandra, är de jämnt fördelade mellan det minsta och det största värdet eller ligger de flesta i en klump precis ovanför det minsta värdet? Medelvärdet eller medianen bidrar till viss del med info om detta, men det finns fortfarande en rad olika kombinationer av värden som kan ge upphov till de resultat vi har fått.
Med andra ord, ibland kan det vara så att olika statistiska material har samma antalet observationer och får samma medelvärde, samma median och samma variationsbredd trots att de skiljer sig rätt mycket från varandra vad gäller undersökningsresultat.
Så hur kan man på ett bättre sätt mäta spridningen för att få ett hum om skillnaden mellan dem?
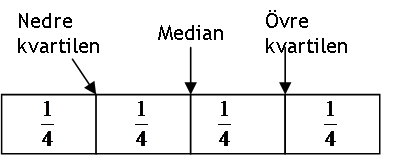
Jo, genom att beräkna kvartilavståndet. Kvartilavståndet får man fram med hjälp av tre värden som kallas kvartiler. Kvartilerna delar in materialet i fyra lika stora delar. Medianen är den mittersta kvartilen och sedan har vi den övre och undre kvartilen.
Om vi ska bestämma kvartilavståndet för respektive klass så börjar vi med att rada upp resultaten för respektive klass i storleksordning och markerar medianen samt den övre och nedre kvartilen:
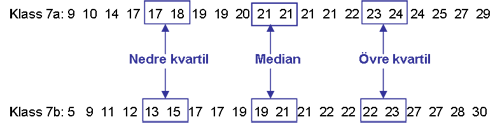
I detta fall hamnar både medianvärdet och kvartilerna mittemellan två värden. Alla beräknas genom att de båda värdena läggs ihop och sedan delas med 2 (dvs medelvärdet av de båda talen).
Klass 7a:
Klass 7b:
Kvartilavståndet för klass 7a är och för klass 7b . Här får vi nu värden som något bättre visar spridningen inom klasserna samtidigt som den tagit hänsyn till fördelningen av resultaten något mer än vad variationsbredden gör.
I de flesta fall är det alltså bättre att ange den nedre och övre kvartilen framför variationsbredden, eftersom variationsbredden bestäms enbart av det största och minsta värdet och kan då lätt bli missvisande.
På en arbetsplats arbetade 14 personer, nedan visas deras åldrar.
19 19 20 22 23 24 24
26 26 28 38 42 45 53
Beräkna de tre kvartilerna
Medianen är normalt det tal som står i mitten, men eftersom vi har ett jämnt antal åldrar så finns det ingen mitt. Då tar man istället och lägger ihop de två tal som är vid sidan om mitten och delar deras summa med 2. I detta fall är det 24 och 26 som är de båda ”mitten-talen”.
Den undre och övre kvartilen får vi genom att först dela in de 14 talen i två lika stora grupper, vilket nästan redan är gjort i uppgiften. Den övre raden är de minsta talen i stigande ordning och den undre raden är de större talen som fortsätter den stigande ordningen, det är 7 tal på varje rad. Så då är det bara att läsa av mittentalet i varje rad.
Den undre kvartilen blir 22 då 22 är det mittersta talet i den övre raden.
Den övre kvartilen blir 38 då 38 är det mittersta talet i den undre raden.
Svar: Md=25, den undre kvartilen är 22 och den övre kvartilen är 38.
Lådagram
Ett lådagram är ett grafiskt sätt att presentera spridningsmåtten på, hur det är uppbyggt ser vi i bilden här nedanför.
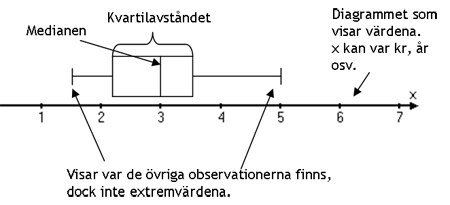
Lådans vänsterkant representerar den nedre kvartilen medan dess högerkant representerar den övre kvartilen. Detta innebär att lådans längd motsvarar skillnaden mellan undre och övre kvartilen det sk. kvartilavståndet.
De båda linjerna som är dragna från lådans vänster respektive höger kant visar att det finns värden som ligger utanför den undre respektive övre kvartilen. Det finns dock en gräns för hur långt man kan dra de linjerna. Man kan alltså inte bara dra den vänstra linjen ända bort till det lägsta värdet och den högra linjen ända bort till det högsta värdet i talserien. Ibland är det så att det existerar extremvärden. Extremvärden är de observationer som ligger mer än 1,5 kvartilavstånd under den nedre kvartilen alt. över den övre kvartilen.
Nedre kvartilen – 1,5*kvartilavståndet = den undre gränsen
Övre kvartilen + 1,5*kvartilavståndet = den undre gränsen
För att ta reda på var gränserna går tar i den nedre kvartilen minus 1,5*kvartilavståndet och sedan den övre kvartilen plus 1,5*kvartilavståndet. Vi har då fått en undre och en övre gräns. Linjerna dras alltså till det värde som ligger närmast inom den undre respektive övre gränsen. Skulle vi nu ha ett värde som underskriver alt. överskrider dessa gränser så kommer det att kallas extremvärde. Extremvärden märks ut i diagrammet som en stjärna * där värdet befinner sig på x-axeln.
På en arbetsplats arbetade 18 personer, nedan visas deras månadslöner i kronor.
12 800 13 100 14 900 14 300 15 200 15 300 15 300 15 400 16 000
16 800 16 900 17 200 19 200 21 200 22 500 26 500 27 000 32 000
Visa fördelningen i ett lådagram.
Börja med att bestämma de tre kvartilerna. Medianen är summan av de två mittentalen delat med 2.
Den undre och övre kvartilen får vi fram genom att dela in talen i två lika stora grupper. Grupperna har alltså 9 löner var. Detta är redan ordnat i uppgiften där den övre raden har de 9 lägsta lönerna och den undre raden fortsätter med de 9 högsta.
Den undre kvartilen blir 15 200 då det är det mittersta talet i den övre raden.
Den övre kvartilen blir 21 200 då det är det mittersta talet i den undre raden.
Vidare så kan vi också konstatera att det minsta värdet är 12 800 och det största värdet
32 000.
För att kunna rita lådagrammet börjar vi med att beräkna kvartilavståndet:
21 200 – 15 200 = 6 000
Därefter beräknar vi den undre och övre gränsen:
Undre = 15 200 – 1,5 * 6 000 = 6 200
Övre = 21 200 + 1,5 * 6 000 = 30 200
Detta innebär att den högsta lönen på 32 000 kr är ett extremvärde och kommer att markeras med en stjärna.
Nu har vi all info vi behöver för att kunna rita vårt lådagram:
En ytterligare förklaring av lådagrammet i exemplet ovan:
Lådans vänstra kant visar värdet 15 200 = undre kvartilen.
Lådans högra kant visar värdet 21 200 = övre kvartilen.
Medianen är linjen inuti lådan som visar på värdet 16 400.
Linjen åt vänster markerar värdet 12 800 som är det värde som är lägst och fortfarande befinner sig inom 1,5 kvartilavstånd från den undre kvartilen (gränsen gick vid 6 200).
Linjen åt höger markerar värdet 27 800 som är det värde som är högst och fortfarande befinner sig inom 1,5 kvartilavstånd från den övre kvartilen (gränsen gick vid 30 200).
Värdet 32 000 markeras med en stjärna för det var ett extremvärde, det överskred 30 200.
Lådagram på grafräknaren
Standardavvikelse
Det mesta använda spridningsmåttet är standardavvikelsen. När man vill ha ett mått på hur de olika värdena avviker på från medelvärdet så beräknar man standardavvikelsen.
Sättet att beräkna standardavvikelsen sker i följande 6 steg:
- Börja med att beräkna medelvärdet.
- Beräkna därefter differenserna av observationerna och medelvärdet.
- Beräkna kvadraterna på differenserna.
- Addera ihop kvadraterna.
- Dela den summa du får med antalet observationer minus 1.
- Ta kvadratroten ur kvoten du fick fram i steg 5.
Tipset är att du använder en miniräknare för detta.
7 personer skulle ut och jogga för första gången i sina liv. Så här många km orkade de olika personerna innan de stannade och började gå:
4 2 1 5 8 1 7
Beräkna standardavvikelsen.
Om vi följer listan som står ovanför exemplet så ser vi att första steget är att beräkna medelvärdet. Lägg ihop alla kilometrarna och dela med 7:
Nästa steg är att vi ska ta respektive observation minus vårt medelvärde:
4 – 4 = 0
2 – 4 = -2
1 – 4 = -3
5 – 4 = 1
8 – 4 = 4
1 – 4 = -3
7 – 4 = 3
Steg 3 och 4 tar vi samtidigt. De tal vi fick fram nu ska kvadreras vart och ett. Kvadraterna ska sedan läggas ihop vilket ger:
Denna summa ska vi, enligt steg 5 och 6, dela med antalet observationer minus 1 och sedan ta kvadratroten ur detta tal. Antalet observationer var ju 7, vilket innebär att talet vi ska dela med är 6 (7 – 1).
Svar: Standardavvikelsen är 2,8.
Vad är det då egentligen som standardavvikelsen berättar för oss?
Jo,
- om de olika mätvärdena har liten spridning så blir inte avvikelserna från medelvärdet särskilt stora och därmed blir även standardavvikelsen liten.
- om mätvärdena har stor spridning blir även standardavvikelsen större.
- standardavvikelsen spelar framförallt en stor roll i normalfördelat material (se nästa sida).
Standardavvikelse på grafräknaren
Denna övning finner du under grafräknarsektionen. För att läsa vidare om hur man gör, klicka här.