Matte 3 - Derivata
Räkna med derivata
Derivata – Räkneexempel
Innan vi tittar på hur man tar fram en allmän formel för derivatan utifrån en funktion så tänkte jag att vi skulle börja med ett räkneexempel.
Vi har funktionen eller om man föredrar det, det spelar ingen roll då det bara är olika skrivsätt. I denna funktion har vi en punkt given, nämligen punkten x=2. Denna punkt har y-värdet 4, det vet vi eftersom vi kan ersätta x i funktionen med 2. .
Vi vill nu ta reda på vilken lutning grafen har i just denna punkt.
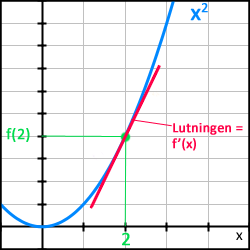
För detta behövs det alltså ytterligare en punkt på grafen. Denna benämns som då den ligger på avståndet h från punkten x=2.
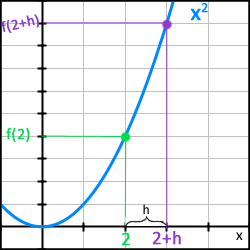
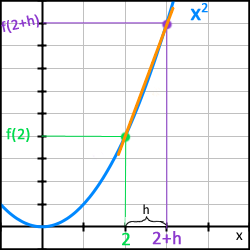
Denna lutning kunde vi alltså beräkna genom att dela skillnaden i y-led med skillnaden i x-led:
Y-värdena är resultatet av att vi tagit respektive x-värde och satt in det i funktionen för grafen, dvs x-värdet upphöjt till 2.
Vi förenklar nu uttrycket så långt det går:
Vi tillämpar gränsvärdet igen, dvs här sätter vi nu att h=0, vilket ger följande:
Lutningen för tangenten i punkten x=2 hos funktionen , alltså derivatan för funktionen i punkten där x=2 är .
Bestämma en funktions derivata
Hittills har vi enbart räknat på derivatan när vi har en punkt på kurvan given. Kan vi få fram derivatan för funktionen oavsett vilket värde vi har på x?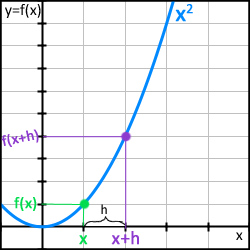 
Vi tittar på vår kurva igen. Denna gång har vi valt punkten x. Kom ihåg nu, derivatan av en funktion är detsamma som formeln för lutningen i en viss punkt på funktionens kurva. Lutningen beräknar vi genom att välja ytterligare en punkt som förslagsvis är på avståndet h från punkten x.
Derivatan definierades ju som
…där funktionen f inte är någon särskild funktion, det kan vara vilken som. I detta fall så vet vi att . Det innebär att om vi hade haft en punkt med x-värdet 4 så skulle y-värdet (funktionens värde) vara lika med 16, vi räknar alltså ut det genom att ersätta x med 4.
f(4)=16.
Nu har vi inte några direkta siffror utan nu har vi istället x-värdena x respektive x+h. Om dessa x-värden sätts in i funktionen så får vi följande:
I täljarens första del så ser vi hur funktionen f(x)=x^2 ser ut om vi ersätter x:et med (x+h) och i andra delen hur den ser ut om x ersätts med x. Vi kan förenkla detta uttryck genom att utveckla parentesen som är upphöjd till 2:
Vi ser att +x^2 och –x^2 tar ut varandra och därtill kan vi dela resterande termer i täljaren med h:et i nämnaren:
Denna formel är ju fortfarande baserad på att vi har använt oss av två punkter i grafen. Om vi tänker tillbaka på begreppet “h går mot noll” så innebar ju det att ju närmare den andra punkten ligger den punkten vi vill beräkna derivatan för desto närmare kommer vi det sanna värdet för denna punkt. Så om h skulle vara lika med noll så skulle lutningen i punkten x vara lika med 2x. Observera att man inte kan sätta h=0 då h fortfarande står i nämnare eftersom division med noll inte är möjligt.
Det vi har gjort nu är att vi har bestämt en generell formel för derivatan för funktionen ! Med andra ord kan vi använda denna formel så fort vi vill veta lutningen i någon punkt längs kurvan som funktionen utgör.
Funktionen har derivatan .
- så får du värdet på kurvan i just den punkten, dvs y-värdet
- så får du veta vilken lutning kurvan x^2 har i just den punkten
För funktionen gäller att .
a) Bestäm med hjälp av derivatans definition .
b) Bestäm, med hjälp av derivatans formel som du fick ut i a-uppgiften,
a) Talet a kan vara vilket tal som helst, det innebär att vi, när vi är klara, kommer att ha en generell formel för derivatan av funktionen .
Derivatans definition kom vi ju fram till förut att den var:
Vi ersätter x:en med talet a:
Det som gäller för denna funktion är att variabeln dels är upphöjd till 2, dels multipliceras med 3. Vi applicerar detta på vår derivatafunktion och börjar att förenkla uttrycket. Kom ihåg att det är två punkter på grafen som det räknas på, dels den med x-värdet a+h, dels den med x-värdet a, båda ska vara upphöjda till 2 och multiplicerade med 3.
och tar ut varandra. Kvar blir:
där vi kan lösa ut h:et i nämnaren:
Nu när nämnaren är borta är det fritt fram att beräkna gränsvärdet genom att sätta in h=0:
Eftersom a kunde vara vilket tal som så kan det lika gärna stå att derivatan till funktionen är
b) Vi ersätter x med 7 i funktionen och beräknar värdet:
Svar: a) b)
20 november 2014 @ 22:12
fuck
26 september 2015 @ 12:51
har någon fattat gränsvärde
samt derivatans definition