Matte A - Geometri
Omkrets och area
Omkrets och area på månghörningar
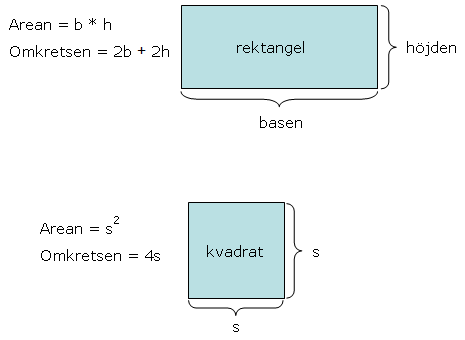
Rektangel
Då vi ska räkna ut arean av en rektangel så multiplicerar vi basen med höjden. Samma sak gör vi med kvadrater som är så kallade liksidiga rektanglar, alltså alla sidorna är lika långa. Detta gör så att kvadratens area är sidan i kvadrat eller sidan upphöjt till 2.
Lille Bosse är ute och gör kullerbyttor på gräsmattan utanför villan han och hans familj bor i. Tomten är rektangulär och har en yta på 1408 m2. Hur bred är tomten om dess längd är 64 meter?
Vi börjar med att rita en figur. Att rita upp det man ska beräkna underlättar mycket och avlastar hjärnan som då kan fokusera mer på beräkningen.
Tomten var rektangulär så vi ritar upp en rektangel och skriver dess area som var 1408 m2. vi fick också reda på att längden (=basen) var 64 meter. Vi ska alltså räkna ut bredden (=höjden) på tomten.
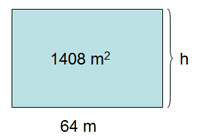
Formeln för arean hos en rektangel säger att basen·höjden=arean. Vi ställer upp den med våra tal som vi vet:
Vi har nu fått en ekvation där vi lätt kan lösa ut h och därmed få reda på bredden.
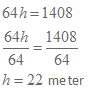
Svar: Tomten är 22 meter bred.
Parallellogram
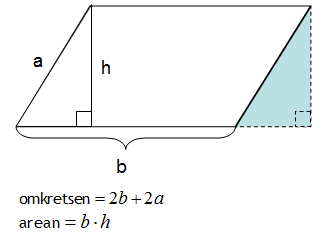
När man ska beräkna arean på en parallellogram, där motstående sidorna är parallella så använder man samma formel som för en vanlig rektangel. Om vi tittar på bilden nedan så ser vi att vi får en rektangel genom att flytta på parallellogrammens sidor, som vi har märkt ut som trianglar. Det viktiga är att du tar ut höjden i parallellogrammen genom att dra en normal från basen och upp.
En parallellogram har sidorna 37,3 mm och 12,5 mm och höjden 10,1 mm (höjden är vinkelrät mot den längre sidan). Bestäm parallellogrammens omkrets och area.
Vi börjar med att rita en figur och märker ut de måtten vi vet. Den längsta sidan var 37,3 mm och det var från den som höjden gick vinkelrätt ut ifrån. Den korta sidan var 12,5 mm.
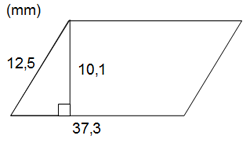
Notera att jag har skrivit mm inom parentes ovanför figuren – ett smidigt sätt att presentera att alla mått i figuren står i mm och så slipper man skriva till det efter varje siffra och riskera att figuren blir kladdig och rörig.
Omkretsen räknar vi ut genom att lägga ihop de fyra sidorna:
Arean är basen gånger höjden, där basen motsvarar 37,3 mm och höjden 10,1 mm.
Svar: Omkretsen är 99,6 mm och arean är 376,7 mm2.
Triangel
Arean för en triangel får vi ut genom att antingen se den som en halv rektangel eller en halv parallellogram. Detta ger oss att arean för en triangel är basen gånger höjden delat med 2.
Beräkna omkrets och area hos triangeln.
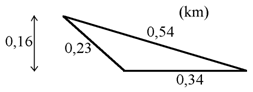
För omkretsen lägger vi ihop de tre sidornas olika längder:
Arean är basen gånger höjden delat med 2. 0,34 km motsvarar basen på triangeln och 0,16 km motsvarar höjden.
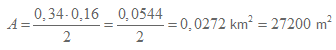
Svar: Triangelns omkrets är 1,11 km och arean är 27200 m2.
Parallelltrapets
Arean av ett parallelltrapets får vi genom att multiplicera höjden med summan av de parallella sidorna dividerade med 2. I bilden nedan ser vi hur vi kommer fram till detta. Parallelltrapetser har bara två parallella sidor. Om vi drar en diagonal delas det i två trianglar och då ser vi att arean för parallelltrapetsen är summan av de båda trianglarnas areor.
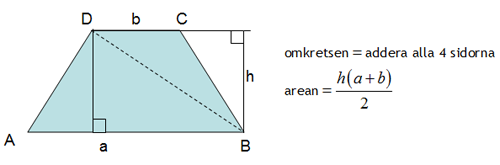
Beräkna parallelltrapetsens omkrets och area.
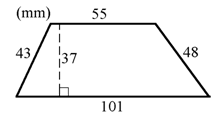
Vi börjar med att beräkna omkretsen som vi får fram genom att lägga ihop de 4 sidorna:
Formeln för arean säger att vi ska addera sidorna a och b och sedan gånga det talet med höjden och till sist dela med 2. Vi ser i figuren att a=101 mm och b=55 mm samt att höjden är 37 mm och kan då sätta in dessa tal i formeln och sedan räkna ut arean:
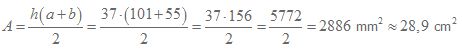
Svar: Omkretsen är 24,7 cm och arean är 28,9 cm2.
Kom ihåg att det gäller andra regler när man skriver om enheter som är i kvadrat! Skulle vi göra om 2886 mm till cm skulle vi, precis som vanligt, flytta kommatecknet ett steg åt vänster och på så sätt få 288,6 cm.
Men då enheterna är i kvadrat så blir ett steg istället lika med 2 steg.
3 m2 t.ex. är lika med 30 000 cm2. 3 m är ju 300 cm, och när det är kvadrerat så tar vi ett steg extra för varje steg, vilket resulterar i dubbelt antal nollor eller decimaler beroende på om man omvandlar till större eller mindre mått.
Romb
En romb är ett speciallfall av en parallellogram. Den ser likadan ut, men skillnaden är att alla sidorna i romben är lika långa. För att få fram omkretsen på en romb lägger du bara ihop alla fyra sidorna och eftersom de är lika långa kan vi säga att vi multiplicerar sidlängden med 4. Arean beräknas på samma sätt som hos en parallellogram.
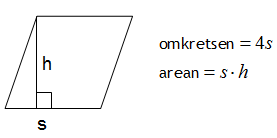
Beräkna rombens omkrets och area om denne har basen 17 cm och höjden 13 cm. (Höjden är vinkelrät mot basen).
Börja med att rita en figur och fyll därefter i med den information vi fått.
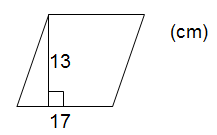
Omkretsen fås genom att multiplicera sidan (17) med 4:
Formeln för rombens area var basen (sidan) gånger höjden, 17 motsvarar basen och 13 motsvarar höjden:
Svar: Rombens omkrets är 68 cm och arean är 221 cm2.
Kvadratrötter
Kvadratroten är motsatsen till att kvadrera, alltså att ta ett tal upphöjt till 2. När man räknar ut kvadratroten på ett tal så blir svaret ett tal som multiplicerat med sig själv blir det tal man tog kvadratroten ur.
Beräkna .
Talen 5 och -5 är båda kvadratrötter ur 25 då båda 52 och (-5)2 är lika med 25.
Anledningen till att x även kan vara ett negativt tal när det gäller kvadratrötter är regeln som säger att minus · minus = plus.
Svar: x1=5 och x2=-5.
Räkneregler för kvadratrötter
Dessa regler gäller om a och b är positiva tal:
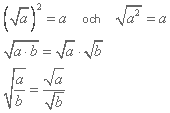
Pythagoras sats
Kan vi använda då vi vill ha reda på längden utav någon av sidorna i en rätvinklig triangel. De sidor som bildar den räta vinkeln i triangeln kallas för triangelns kateter medan den tredje sidan kallas för hypotenusa. I figuren här nedanför ser vi att om vi adderar de båda kateterna i kvadrat så får vi hypotenusans kvadrat.
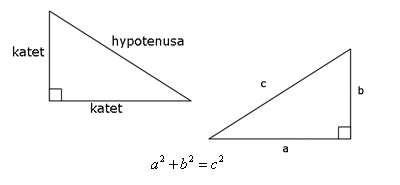
Du har en rätvinklig triangel vars ena katet är 4 cm och den andra 5 cm. Hur lång är dess hypotenusa?
För att få en bättre överblick kan du rita upp triangeln.
Vi benämner hypotenusan med x. Pythagoras sats säger att:
Alltså:
eller bättre
Svar: Hypotenusan är 6,4 cm.
Du har en rätvinklig triangel. Dess ena katet är 3 cm och hypotenusan är 9 cm. Hur lång är den andra kateten?
Beteckna den andra kateten med x. Enligt pytagoras sats så är:
Lös ekvationen och du får svaret.
Svar: Den andra kateten är 8,5 cm.
Notera att i dessa två exempel har jag inte brytt mig om att anteckna att det även finns negativa lösningar på kvadratrötterna. Detta beror på att de båda exemplen handlar om att räkna ut en sträcka, och sträckorna kan ju som bekant inte vara negativa.
Cirklar och sektorer
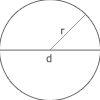Då vi ska räkna ut omkretsen och arean för en cirkel måste vi använda oss av konstanten , som uttalas ”pi”. Ett närmevärde med tre gällande siffror för är 3,14 och med fem gällande siffror blir det 3,1416. De flesta miniräknare har dock en särskild knapp föroch då föreslår jag att du använder den istället. Detta för att få ett så exakt svar som möjligt, och det är bättre att avrunda endast i slutet istället för att göra det redan från början. Då är risken att få fel svar större.
För att räkna ut omkretsen för en cirkel så tar vi diametern multiplicerat med. Diametern är det bredaste stället på cirkeln, man drar ett streck från cirkelns kantlinje, genom mittpunkten och sen fram till stället mittemot det man började. Diametern är samma sak som radien multiplicerat med 2.
Omkretsen för en cirkel är: eller
Arean av en cirkel får vi genom att multiplicera med radien i kvadrat. Radien är halva diametern, det vill säga avståndet från mittpunkten till cirkelns kant.
Arean av en cirkel är:
Hur stor är plåtbitens area (det färgade området) om hålets diameter är 30 mm?
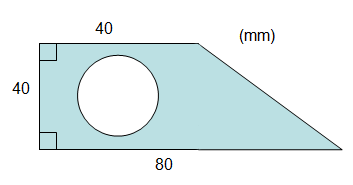
För att få fram plåtbitens area så ska vi ta plåtbitens hela area, alltså om det inte hade varit ett hål där, minus arean av cirkeln.
Börja med att räkna ut plåtbitens hela area. Vi delar in figuren i två delar, en kvadrat och en triangel och döper deras areor till A1 respektive A2.
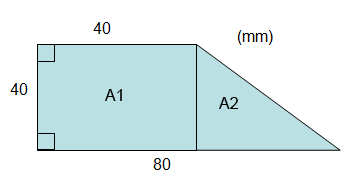
Vi vet att A1 är en kvadrat då figuren anger att både basen och höjden på fyrkanten är 40.
Triangeln har också basen 40 och höjden 40 då vi ser att den är lika hög som kvadraten. Likaså om triangelns och kvadratens baser tillsammans är 80 och kvadratens bas är 40 så måste triangelns bas utgöra de resterande 40.
Den sammanlagda arean (A3) för plåtbiten utan hål är således:
Nästa steg blir att räkna ut cirkelns area. Vi vet att diametern var 30 mm, och därför vet vi också att radien på den är 15 mm (r=30/2), vilket är det enda vi behöver för uträkningen.
Det inringade a:et betyder att jag har sparat det egentliga talet med en massa decimaler i grafräknarens minne på bokstaven A.
Plåtbitens area, det färgade området blir alltså:
Där det inringade a:et anger att jag har räknat ut svaret med det oavrundade talet.
Svar: Plåtbitens area är 1693 mm2.
Cirkelsektorer
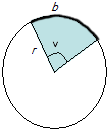En cirkelsektor begränsas av två radier och en cirkelbåge. I cirkeln till höger har vi blåmarkerat cirkelsektorn som har vinkeln v. Andelen av vinkeln v på hela varvet är v/360°.
Cirkelbågens längd är alltså v/360° av cirkelns omkrets. Då vi dividerar vinkeln v med det totala så får vi fram andelen av hela omkretsen. Om vi vill veta hur stor den andelen är måste vi multiplicera andelen med den totala omkretsen.
Längden på en cirkelbåge är:
Cirkelsektorns area får vi fram på samma sätt, fast vi multiplicerar andelen med cirkelns totala area istället.
Area för cirkelsektor är:
En cirkelsektor har radien 1 cm och vinkeln 60 grader. Beräkna dess omkrets och area.
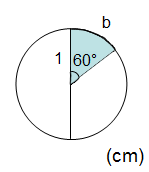Vi börjar med att rita en cirkel med cirkelbågen i sig. Den behöver inte ritas korrekt, det är bara för att uppgiften ska vara enklare att överblicka.
Omkretsen räknas ut genom att vi lägger ihop längden av de tre sidorna som utgör cirkelbågen, nämligen de två raka och sedan den böjda sidan. Uppgiften säger att radien är 1 cm, vilket innebär att vi redan fått veta längden på de båda raka sidorna och behöver nu alltså bara beräkna cirkelbågens längd för att kunna få fram cirkelsektorns omkrets.
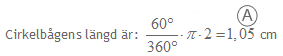
2:an är diametern som vi får fram genom att dubbla radien som ju var 1 cm.
Svaret innehåller egentligen en faslig massa decimaler, men som ni ser så har jag avrundat det och satt bokstaven A efter talet vilket betyder att jag har sparat hela talet i grafräknarens minne på bokstaven A, (se grafräknarsektionen), så att jag kan använda det senare.
Nu vet vi alla sidorna på cirkelsektorn och kan då räkna ut omkretsen:
(A visar att jag räknat ut omkretsen med det oavrundade talet.)
För arean så vet vi redan de tal som behövs; vinkeln v och radien r.
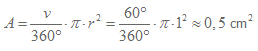
Svar: Cirkelsektorns omkrets är 3 cm och arean är 0,5 cm2.
29 juni 2010 @ 11:10
Hur räknar man ut diametern om man endast har omkretsen?
29 juni 2010 @ 14:49
Omvänd räkning dvs omkretsen delat med pi
17 juli 2010 @ 18:48
Hej! Jag är svårt för detta att räkna ut omkretser och area när det är furkanter som det sticker ut en tekant på. Hur kan man göra detta enkelt för sig att räkna ut?
17 juli 2010 @ 19:52
Man delar upp det… se exempel 9
26 juli 2010 @ 13:31
Hur man beräkna ramens area av en tavla?
26 juli 2010 @ 23:59
Läs högst upp på sidan så ser du. Tavlan är kvadratsk, Area=höjeden * bredden
17 augusti 2010 @ 23:18
Var kan man läsa om hur man räknar ut volymen på respektive former??
18 augusti 2010 @ 2:08
Hej!
vad jag har fått veta utav er är att när man räknar ut sidan genom arean så tar man b * h. Men om arean är t.ex. 6,76 cm2 och b * h ska man ränka ut själv. Då blir ju ekvation så här:
x * x = 6,76.
x2 = 6,76. Då får man ju inget svar?
18 augusti 2010 @ 17:27
Nils: Kolla formelbladen till nationella proven. http://www.matteguiden.se/nationella-proven/formelblad/
Kurt: Jag antar att du menar en kvadrat. x * x = 6,76 => x^2 = 6.76. Ta då roten ur 6.76 så får du vad en sida är.
22 september 2010 @ 12:57
Hej!
Behöver hjälp med en uppgift då jag är lite ringrostig i matten.
vi vet att rektangelns kortsida är 20 cm kortare än långsidan. arean är 4800 cm2. Hur får jag fram svaret?
Får fel varje gång jag försöker…
22 september 2010 @ 22:08
Sjuk bra sida tack så hemskt mycket nu kan jag typ dubbelt så mkt mer än vad jag kunde förut
MVH Alexander
23 september 2010 @ 7:59
Hej Hanna!
Sådana här frågor hänvisas egentligen till forumet.
Eftersom du vet förhållandet mellan sidorna i rektangeln, dvs att den korta sidan är 20 cm kortare än den långa så kan du säga att den långa sidan är x cm och den korta sidan är x-20 cm.
För att beräkna arean på en rektangel multiplicerar man längden med höjden. Vi vet ju redan arean och kan då ställa upp en ekvation:
x*(x-20)=4800
sen är det bara att lösa ut x så får vi veta hur lång den långa sidan är, och den korta sidan beräknas genom att ta värdet på x minus 20.
20 oktober 2010 @ 16:43
Har ni inte skrivit fel under Exempel 3: räkna ut omkrets och area hos en triangel.
Ni skriver att: 0,0272km2 = 27200m2
men hallå när blir 0km 27.000m?
1km = 1000m, alltså har ni glömt ett kommatecken. (27,200m2)
20 oktober 2010 @ 17:34
Hej Chastity!
Jag tror att räkningen är rätt gjord… Men man kan inte säga som du säger 0km != 27000m , men 1km^2 = 1000 000m^2
Hoppas kommentaren var till hjälp!
21 oktober 2010 @ 20:35
Hur räknar man ut omkretsen om man bara vet resultatet av arean?
9 november 2010 @ 16:10
jag undrar hur man räknar ut arean på ett rör med lock.
till exempel en konservburk
10 november 2010 @ 6:40
@Hanna:
Det beror på, om det är en cirkel så ta först reda på radien genom att dela på pi och sen köra roten ur..
@Alice:
Tänk dig att du tar bort locket och botten. Sen skär du upp röret. Då har du två cirklar och en fyrkant. Fyrkantens sidor är höjden på konservburken och omkretsen på en cirkel.
11 november 2010 @ 19:25
Hejsan ska ha prov imorn och jag undrar hur räknar man ut omkretsen på en kvartscirkel dvs halvcirkel??????
13 november 2010 @ 17:38
Hej Madeleine. Frågor som denna får du nog snabbare svar i forumet.
Om du har omkretsen på en hel cirkel är det bara att dela med 4 för att få en kvartscirkel…
17 november 2010 @ 21:25
Jag undrar hur stor är cirkelns radie om omkretsen är 21cm.
17 november 2010 @ 22:03
@Rikina
Fråga i forumet.
19 november 2010 @ 11:19
Ett badkar har formen av ett rätblock med måtten 1,2 m 50 cm 70 cm. Hur många liter vatten rymmer badkaret?
Hur gör jag?
19 november 2010 @ 11:21
I en park finns det en cirkulär damm som har arean 380 m2. Erik springer runt dammen. Hur långt springer han?
19 november 2010 @ 17:17
Precis som Tobias sa Isak. Fråga i forumet =)
24 november 2010 @ 18:29
En kvadrat ABCD är inskriven i en rätvinklig triangel. Hur beräknar man kvadratens sida då man vet att kateterna är 12 och 18 ?
31 december 2010 @ 19:58
ursäkta jag undrar bara om nationella provet för den här året är svårt eller inte ni vet inte hur det känns för mig jag är obeskrivligt rädd svara mig snälla!!!!!!
1 januari 2011 @ 23:32
Nationella proven är inget man behöver vara rädd för.
Det är samma svårighetsgrad på alla nationella prov. DVS, de är lika lätta/svåra varje år.
10 januari 2011 @ 20:08
Hej har lite problem med en uppgift.
“En guldring har en yttre omkrets som är 56mm. Ringen är överallt 1mm tjock. Hur stor diameter har öppningen i ringen? Avrunda till hela millimeter.”
Krånglig :\
11 januari 2011 @ 1:58
Du får bättre svar i forumet, jag lovar
12 januari 2011 @ 17:29
hej vet någon vad som kommer i den här matte nationella provet.?????
snälla hjälp om ni vet vad som kommer!!!!!!!!
24 januari 2011 @ 20:12
Hej kan ni snälla hjälpa mig jag har prov imorn!
Hur räknar man ut en halvcirkels area?
24 januari 2011 @ 23:16
@Sara:
Räkna ut en helcirkels area och dela med 2. Svårare än så är det inte..
30 januari 2011 @ 16:23
jag har 2 frågor, snälla jag har prov på tisdag !!!
arnold lyckades rita tre trianglar med samma area: det fanns en rätvinklig, en likbent och en trubbvinklig triangel. hur gjorde han?
en kvadrat har sidan 5 cm.
a)förklara hur du räknar ut det färgade områdets area ( svaret är 5,375 cm2
b) förklara hur du kommer fram till att 21,5 % av den totala arean är färgad?
tacksam för svar !
1 februari 2011 @ 20:06
Hej
jag undrar bara om det finns någon bra hemsida om rymd geometri.
2 februari 2011 @ 13:57
Bästa siden ever ja svär
27 mars 2011 @ 22:20
Om man ska skriva diametertecknet skriver man det före eller efter sifrona?
31 mars 2011 @ 21:21
“rita en rektangel med basen 7 cm och höjden 3 cm. beräkna sedan rektangelns
a) area
b) omkrets
31 mars 2011 @ 21:21
jag förstår inte hur jag räknar det
31 mars 2011 @ 21:22
Läs från forumen!
4 april 2011 @ 14:17
Går det att räkna ut längen på en cirkelkurva med hjälp av radien och avståndet mellan början och slutet på kurvan?
5 april 2011 @ 11:50
hej, sorry att vara irriterande men snälla kan du lägga upp en del om AREAENHETER. Jag minns ingenting från grundskolan och det skulle nog hjälpa många om det fanns. För plötsligt out of nowhere börjar du skriva om svar som går från km2 till m2 utan att man fått gå igenom omvandlingen av dem.
ta det här som kärleksfull kritik
7 april 2011 @ 10:01
Om jag bara vet Arean på cirkeln.
Hur räknar jag ut arean till ett Borrhål.
Tex. Jag har två hål som har tillsammans 34.70 Area som leder kylvatten.
Om jag nu skall bättra på kyleffekten med tre nya kanaler till in i cylinerns yttterkyl väggar så får motståndet inte blir lägre än huvud kanalerna då kraften alltid tar den lättaste vägen.
Alltså. Jag har två hål med 4.7mm tillsammans har de en Area på 34.70 Area.
Då väljer jag att modifiera cylindern och motorblock med tre kanaler till och jag vill ha 3 hål och väljer talet 30 delat på 3 = 10 area.
Hur räknar Area 10 till borrets millimeter diameter.
10 april 2011 @ 15:25
Hej jag heter adam jag har inga vänner, så jag räknar matte på dagarna!
Så hör av er till mig om ni behöver hjälp! 
25 april 2011 @ 8:45
Det var bra visste redan lite men det var bra. Jag jobbar. Med detta nu i matteboken
9 maj 2011 @ 21:55
Hejsan!! Om arean är 200 000m2, hur stor är då diametern??? snälla hjälp mig!!
17 maj 2011 @ 19:00
då blir den 20
23 maj 2011 @ 17:00
Jag behöver hjälp med läxan!!!
Kan inte komma på några exempel på när man behöver kunna mäta omkretsen på T.ex en kvadrat.
Snälla, hjälp mig!!!
30 juni 2011 @ 13:35
Skall räkna ut area på en bult.
Hur gör man??
Tack tack
22 september 2011 @ 11:15
hur räknar man ut arean på en lunga??
22 oktober 2011 @ 18:06
hur beräknar jag radien av en cirkel om jag bara har har arean?
26 oktober 2011 @ 21:27
heej snälla kan ni hjälpa mig hur lång omkrets har halvcirkeln?
2 november 2011 @ 1:34
Hej!
Jag har lite matteproblem och önskar att du kunde skicka ett svar till mig via min e-postadress.
Mattefrågan:
Två trianglar är likformiga. Beräkna x och y.
Den ena triangeln har sitt x på sidan längst ner och på vänster sida 40 cm och på höger sida 56 cm.
Hur beräknar jag x på denna triangel?
Jag vet att vilkelsummorna i en triangel alltid ska vara 180 grader..men jag vet inget om sidorna.
Tack.
15 november 2011 @ 12:43
Hur gör man om omkretsen på ett klot till area?
T.ex: “Jorden är nästan klotformig. Räkna ut jordens yta om ekvatorn är cirka 4000 mil.”
Hur gör jag då??
20 november 2011 @ 18:56
hur räknar man ut omkretsen på en prisma? skulle vara bra om någon kunde hjälpa mej!?
(Y)
22 november 2011 @ 22:13
hur räknar man ut arean om man bara vet huur lång diametern är?
24 november 2011 @ 19:08
hur räknar man ut omkretsen på en prisma? skulle vara bra om någon kunde hjälpa mej!? (Y)
5 december 2011 @ 14:07
Joachim det beror väldigt mycket på vilken typ av prisma du har. det finns tresidiga prismor som beräknas som trianglar, fyrsidiga prismor osv. Utav dessa kan prismor vara regelbundna och oregelbundna, dessutom kan en prisma vara rätvinklig, snett och konvexa. är det omkretsen av baserna som du ska beräkna så bör du först ta reda på vilken typ av prisma du ska beräkna omkretsen på och utefter det välja rätt metod för att beräkna omkretsen.
5 december 2011 @ 14:22
H, det finns ett bra exempel på hur du beräknar det här på matteguiden.
http://www.matteguiden.se/matte-a/geometri/kroppar/
4000/π/2 = r
4*π*π^2 = arean av ett klot
i ditt fall borde det bli ca 5,092,958
5 december 2011 @ 14:26
mimmi ta diametern dela med 2 så får du radien för att beräkna arean använder du följande formel 4*π*r^2 = arean av ett klot
förlåt H det blev fel när jag skrev formeln för dig det ska vara samma som för mimmi här.
5 december 2011 @ 14:32
Yasmin kan du inte använda pytagoras sats för att beräkna det?
a^2 + b^2 = c^2
ta sen roten ur c^2 för att få fram längden på c.
ex. 40^2 + 56^2 = 4736
roten ut 4736 = ca 68.82
8 december 2011 @ 14:54
Hej!
Någon som vet hur man räknar “Pythagoras sats” men istället för hypotenusa (X) om man vill sätta ex. 49????
Tusan tack
17 december 2011 @ 20:26
Hur räknar man ut basen o höjden om man bara vet arean på ett föremål?
T ex en ödla ska ha ett terrarie på minst 20 kvadratdm, hur vet jag då hur långt och högt terrariet måste vara?
31 januari 2012 @ 20:37
tack för hälpen
31 januari 2012 @ 20:45
jag har räknat area på en triangel som är tex.. 5 cm på ena sida och 3 cm på andra sida och fick 7,5 cm på på långa sidan men om jag ritar på riktig så får jag 5,8cm på långa sidan varför
6 februari 2012 @ 22:26
TACK
22 februari 2012 @ 13:46
Tack!
22 februari 2012 @ 13:46
Tack!
27 februari 2012 @ 18:07
TACK!
6 mars 2012 @ 18:44
Hej, jag går u 7:an och behöver hjälp med hur man kan räkna en figurs area? och behöver jag hjälp med x trianglar
4 juni 2012 @ 12:02
[...] nyckeln till att förklara svåra begrepp på ett enkelt sätt. Se till exempel detta avsnitt om Area och Omkrets. Kan det bli mer pedagogiskt än så? This entry was posted in Okategoriserade. Bookmark the [...]
5 juni 2012 @ 18:03
tack för hjälp…<3
21 augusti 2012 @ 7:31
Någonstans måste du ha räknat fel. Jag försöker hitta hur men lyckas inte. Om du räknar på en enkel räknare måste du tänka på att räkna stegvis och inte från vänster till höger (fast det känner du säkert igen) det brukar annars vara vanligaste felet. Lycka till med ditt räknande och fortsätt att konstrollera om dina resultat är rimliga.
21 september 2012 @ 7:41
En triangel med en sida på 3 och en sida på 5 blir alltid svaret 4 på den tredje sidan!
8 november 2012 @ 20:37
Vad är arean av en cirkel diameter med 16 och 50 cm?!
19 januari 2013 @ 16:14
tack för hjälp ♥.
30 januari 2013 @ 12:51
AHAAAAA
24 februari 2013 @ 15:16
Nej du. Har du en triangel med ena sidan 3 och den andra sidan 5 och vill räkna ut diagonalen använder man sig av pythagaros sats. a2 + b2 = c2, vilket ger (3)2 + (5)2 = c2. Alltså 9 + 25= c2. Vilket ger c2 = 34. c blir då roten ur 34, vilket är ungefär 5,8 på hypotinusan.
Vill du bara veta arean är det längden gånger bredden delat med 2.
3 gånger 5 delat med 2=7,5
16 september 2013 @ 15:23
tack för din hjälp. ska köpa något fint till mig själv
22 april 2014 @ 20:48
TACK FöR HJäLPEEEEEEEEEEEEEEEEEEEEEEEEEEEN
1 juni 2014 @ 10:37
Kan någon hjälpa mig?
I en rättvinklig triangel är omkretsen 40 cm och en katet 8 cm. Hur lång är triangelns hypotenusa?
6 juli 2014 @ 19:48
Jag vet att omkretsen på en cirkelrund byggnad är 16 meter. Hur stor är arean?
20 november 2014 @ 9:23
På triangel så måste du använda dig av Pythagoras sats
20 november 2014 @ 9:25
Korrigering du tar basen delat på höjde
25 november 2014 @ 3:40
Exempel 9 är så oproportionerlig att jag inte ens vet vad jag ska säga om det xD Helt värdelös ritning även om själva uträkningen var korrekt.
7 december 2014 @ 15:25
Jag vill fråga en sak och hoppas ni kan väll svara : frågan är Hur mycket större är kvadraten än cirkeln om basen är 3 m?
16 januari 2015 @ 9:10
Förhållandet mellan sidorna i en tv-apparat är 16:9. Om en viss tv är 82 cm bred, hur hög är tv:n?
16 januari 2015 @ 9:13
Förhållandet mellan sidorna i en tv-apparat är 16:9. Om en viss tv är 82 cm bred, hur hög är tv:n?
10 maj 2015 @ 11:42
Tackar
12 maj 2015 @ 8:04
beräkna area och omkrets av en rektangel med sidorna 3,5 cm och 8 cm
7 juli 2015 @ 21:34
Jag har en uppgift som jag inte förstår hur jag ska räkna ut…
"En rektangels längd är 40% större än dess bredd. Rektangelns area är 35cm². Beräkna rektangelns längd och bredd"
Hur gör man??
8 oktober 2015 @ 23:01
b*h=35cm2
7cm*5cm=35cm2
7/5=1.4
längden 7cm är 40% större än bredden 5cm.
9 maj 2016 @ 20:27
Jag kunde inte räkna den är uppgiften:
Figuren består av 5 kvadrater med lika stor area.
Hela figurens area är 405 cm2
. Bestäm omkretsen av hela figuren.
kan nån hjälpa mig?
27 maj 2016 @ 4:53
Tack så himla mycket!
16 november 2017 @ 10:33
[...] (Kort förklaring) – beräkna arean av rektanglar, parallellogram, trianglar och cirklar (Hur beräknar jag arean?) – använda de vanligaste areaenheterna (Omvandla areaenheter online) – använda skala [...]