Matte A - Geometri
Volym
Volym och begränsningsarea av rätblock, prismor och cylindrar
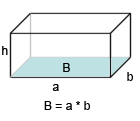
För att få ram volymen av ett rätblock multiplicerar vi bottenarean B med höjden. Man kan även säga att längden gånger bredden gånger höjden. Samma formel gäller även för prismor.
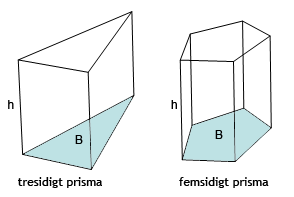
Var dock uppmärksam på att en tresidigt prisma t.ex. har en triangel som botten och du måste således använda formeln för en triangels area då du beräknar B. Likaså måste du uppmärksamma att en femsidigt prismas bottenarea består av både en rektangel och en triangel vilket gör att du måste kombinera areaberäkningsmetoderna för denna.
Begränsningsytorna är de ytor som formar kropparna. I en tresidig prisma t.ex. så är det två trianglar tillsammans med ett antal rektanglar som utgör begränsningarna i formen, medan ett rätblock enbart har rektanglar som begränsningar.
Mantelyta är den yta som är välvd i exempelvis en cylinder eller en kon.
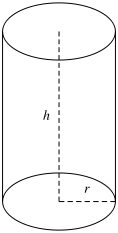Då vi beräknar en cylinders volym får vi dock tänka på en sak; dess bottenarea skiljer sig. Här kan man inte ta längden multiplicerat med bredden, utan botten är cirkelformad. Alltså får vi ta formeln för hur man räknar ut en cirkels area och sedan multiplicera den med höjden på cylindern.
Om vi ska räkna ut cylinderns mantelyta (den välvda ytan på cylindern) så multiplicerar vi basytans omkrets med höjden. Det är lättare att förstå om vi vecklar ut cylindern så att den blir till en rektangel istället. Längden på rektangeln är den ursprungliga omkretsen av cirkeln.
Kubikrötter
Om en kub ska ha volymen 27cm3 så måste kubens sidor vara 3 cm då 33 är 27. Detta innebär att talet 3 är kubikroten ur 27. Då man ska räkna ut kubikroten krävs det oftast en miniräknare. Då är det den här symbolen man ska leta efter:
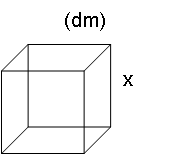En låda som är kubformad rymmer 120 dm3 vatten. Hur långa är dess sidor?
Börja med att rita upp en kub. I en kub är alla sidorna lika långa.
Antag: Sidan är x cm.
För att räkna ut kubens volym tar man ju sidan &middaot; sidan · sidan, alltså:
För att lösa ut x måste vi ta kubikroten ur 120:
Svar: Kubens sidor är 4,9 dm.
Volym och begränsningsarea av pyramider, koner och klot
Volymen för de olika figurerna här nedan får vi genom att räkna ut deras bottenarea, multiplicera den med höjden och sedan dividera med tre.
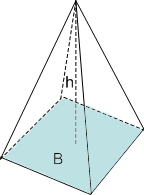
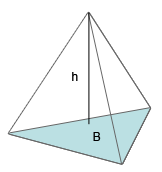
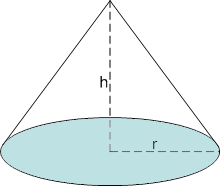
Längst till vänster syns en fyrsidig pyramid, i mitten en tresidig pyramid och längst till höger en kon.
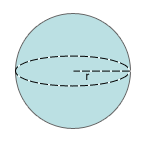
Bilden under de tre övre bilderna visar ett klot med radien och diametern utmärkta. Arean av ett klot innebär dess mantelarea, alltså ytan runt klotet.
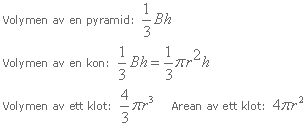
10 december 2010 @ 6:57
Bra, men skulle behövt veta hur man räknar ut kubikroten ur något utan miniräknare.
Försöker komma på hur man ska räkna ut den här uppgiften: “En kub har volymen 27 cm3. Hur stor blir volymen om man gör sidorna 3 gånger så långa?”
Mvh Axel
4 januari 2011 @ 20:04
hej
kan jag få hjälp
varför volym på en Pyramid är mutlti med 1/3 och inte 1/2 …. om volym på en prima är=B.H så skulle gissa att Pyramid är =1/2.B.H och inte 1/3.B.H ?
kan ni förklara detta är ni snäll
23 januari 2011 @ 19:13
Om du tar en kub och ritar in alla rymddiagonaler så får du sex pyramider med en basyta samma som kuben. Då är varje kub en sjättedel av en hel kub, men tre pyramider bildar ett rätblock stort som en halv kub, pch då varje pyramid har en höjd som en halv kub så ser man att det ryms tre pyramider i motsvarande rätblock med volymen bxh.
24 maj 2011 @ 9:52
“Bilden under de tre övre bilderna visar ett klot med radien och diamtern”.
Knappast. “diamtern” är felstavat, ni menar troligen “diametern”. Den torde vara dubbla radien. Det ni visar skulle kunna vara omkretsen av klotets midja, och den är 2*PI*radien…
Noll poäng. UK.
25 maj 2011 @ 15:14
Stavfelen ordnade! Tackar!
11 juli 2011 @ 20:44
Tja. Undrar om någon kan hjälpa mig att räkna ut kvadraten på en triangel med B = 9m och dom andra sidorna är 5.90 m.
Vet att man annars tar b*h/2 men nu vet jag inte höjden på triangeln.
Tack.
15 september 2011 @ 20:52
Fixa fakta om det t.ex hur många kvadrater det finns och massor
2 oktober 2011 @ 20:39
rita upp triangeln och dra en höjd mät den!
5 oktober 2011 @ 19:55
Vet nån varför man ska dela med 3 efter att man räknat ut b*h på en kon? (alltså för att få dens volym), varför måste man dela på 3??
/Tacksam för svar!
28 november 2011 @ 20:36
det är väll för att den är i 3 dimensioner.
24 oktober 2012 @ 21:55
Hur får man ut omkretsen av en kon om man vet att höjden är 4.0 dm och volymen 2.5^3-. Man ska få ut omkretsen ur konens insida i cm….
28 november 2012 @ 16:30
Jag hittar inte vad dm är ..
23 januari 2013 @ 14:12
plz help i need a gf
19 december 2013 @ 12:56
1 dm = 1 decimeter = 1/10 m = 0,1 m = en tiondels meter
mikro = en miljontedel
milli = tusendel
centi = hundradedel
deci = tiondel
-
deka = tio gånger
hekto = hundra gånger
kilo = tusen gånger
exempel en kilogram är tusen gånger en gram alltså tusen gram
God Jul
19 december 2013 @ 13:03
En kon är som en glassstrut. Den har en basyta som är en cirkel och så kan den vara rak eller sned, men volymen är V = B h /3 ( en tredjedel av basytan gånger höjden ). Om man trixar litet med sambandet får man att basytan B = 3 V / h ( tre ggr volymen delat med höjden. ). Och så vet vi att basytan B = pi R^2 varav efter trixande att radien är kvadratroten ur B/pi. Nu blir omkretsen av basytans cirkel diametern ggr pi = 2 pi R = 2 pi ( kvadratroten ur (3 V / h) / pi ).
19 december 2013 @ 13:07
Litet förenkling ger sedan att omkretsen av basytan = kvadratroten(12V pi / h ).
19 december 2013 @ 13:29
V=frac{B cdot h}{3} = frac{(pi cdot r^2 )cdot h}{3} \ \
r^2 = frac{3 cdot V}{pi cdot h} Rightarrow r = sqrtfrac{3 cdot V}{pi cdot h} \ \
Omkrets = 2 cdot pi cdot r = sqrtfrac{12 cdot V cdot pi}{h}
22 augusti 2014 @ 9:37
thank you for the help!
24 augusti 2014 @ 20:16
Dominika Karlsson wth??????
5 oktober 2014 @ 15:49
En låda har formen som ett rätblock och har bottenarean 30 cm2. Hur stor omkrets har lådans botten? tre olika alternativ. hjälp ?!?
18 januari 2015 @ 15:53
lite oklart det där med formeln om konen eller?
18 januari 2015 @ 15:54
eller betyder det bara att konens volym är en tredjedel av basen*höjden, jätteförvirrad, hjälp någon?
2 februari 2015 @ 22:33
30 cm2 = 3 cm x10 cm = 6 cm x 5 cm = 2 cm x 15 cm
Omkrets = 2a+2b = 26 cm el. 12+10 =22 el 4+30=34
4 mars 2015 @ 0:35
Jag behöver hjälp med den fråga
4 mars 2015 @ 0:39
Hej. 6.) En 50 cl konservburk har diametern 64,0 mm och höjden 155,5 mm. Hur mycket aluminiumplåt skulle man spara vid tillverkning av två miljoner burkar om man istället hade diametern 108,4 mm och höjden 54,2 mm? Svara i m2 och avrunda ditt svar till tiotal. Obs! Skriv enheten med bokstäver (alltså kvadratmeter) i svarsrutan.
21 mars 2015 @ 12:25
ett cementrör är 12 meter långt,innerdiametern är 35 cm och röret är 10cm tjockt. hur mycket cement gick åt till att göra röret? Svara i dm3..
31 augusti 2015 @ 15:59
En låda har formen som ett rätblock och har bottenarean 30 cm2. Hur stor omkrets har lådans botten? tre olika alternativ. fattar inte kan jag få hjälp
17 januari 2016 @ 17:38
sidoytor har ett prisma som har en femhörning som basyta hjälp mig med frågan??
25 januari 2016 @ 19:04
Varför är det b*h/3
25 januari 2016 @ 19:05
?
26 januari 2016 @ 10:26
Vad står 4 för i formeln för sfären volym?
29 februari 2016 @ 12:31
Från hur många mobiler behöver man ta tillvara guld för att få ihop till en guldtråd med diameter 1 mm och längd 2 dm ? HJÄLP
28 mars 2016 @ 12:10
Jag vill räkna ut sidan på en triangel i pyramidform. Nån som kan hjälpa mig. Totalblock.
5 april 2016 @ 10:03
Vad är volymen hos ett klot med radien 5 centimeter?
"Hjärnblockad …"