Matte A - Grunder
Tal i decimalform
Positiva tal
Varje siffra i ett tal har ett platsvärde. Med hjälp av platsvärdet vet man hur ett tal är uppbyggt och hur det utläses. Ta till exempel 678, alla vet vi ju hur man utläser detta tal ? sexhundrasjuttioåtta. Skulle man skriva det i en utvecklad form skull det se ut så här:
678 = 6 * 100 + 7 * 10 + 8 * 1
Här visar man att sexan har platsvärdet 100, sjuan platsvärdet 10 och åttan platsvärdet 1. Tar man ett tal i decimalform blir resultat så här:
2,14 = 2 * 1 + 1 * 0,1 + 4 * 0,01
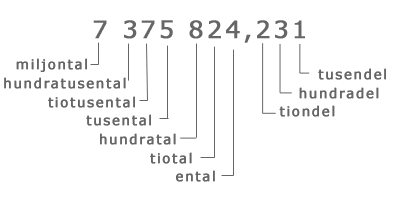
Negativa tal
Dessa används i många olika sammanhang, t.ex. temperaturen kan vara -6°C. Man säger att talen 2 och -2 är motsatta tal, precis som 3 och -3 eller 12 och -12 är motsatta tal. Med hjälp av detta kan man förklara begreppet subtraktion genom att man adderar med det motsatta talet.
Här nedan adderar vi -2 respektive -8 till 7 respektive 6.
Det finns vissa regler som gäller för negativa tal. Reglerna är nödvändiga för att man ska kunna räkna med dem.
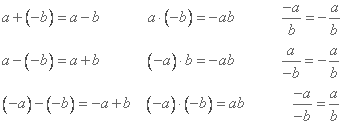
Enligt reglerna ovan så blir två stycken minus plus istället:
Udda och jämna tal
Alla heltal är antingen jämna eller udda. De jämna definieras som de tal som är jämnt delbara med två, annars är de udda. Exempel på jämna tal är …-8, -6, -4, -2, 0, 2, 4, 6, 8… Notera att även noll är ett jämnt tal då 2*0 = 0. Exempel på udda tal är …-7, -5, -3, -1, 1, 3, 5, 7…
Primtal
Det är inte alltid lätt att hålla reda på alla termer och uttryck som används inom matematiken, men ni kanske någon gång har hört talas om primtal? Primtalen är lite speciella, de är nämligen inte jämnt delbara förutom med sig själva och siffran 1. De första primtalen är 2, 3, 5, 7, 11, 13 etc. Notera att talet 2 är det enda jämna primtalet (se udda och jämna tal).
Gällande siffror
Då man ska bestämma antalet gällande siffror i ett tal finns det vissa regler man måste följa.
- Nollor inuti ett tal räknas som gällande siffror.
- Nollor i början av ett tal är inte gällande siffror.
- Nollor i slutet av ett tal med decimaler räknas som gällande siffror.
- Nollor i slutet av ett heltal kan vara gällande, det varierar från fall till fall.
Bestäm antalet gällande siffror i talet
a) 204
b) 8,040
c) 54 790
d) 0,034
a) Då vi vet att nollor inuti ett tal är gällande så har talet 204 tre gällande siffror.
b) Eftersom nollor i slutet av ett decimaltal räknas som gällande så har talet 8,040 fyra gällande siffror.
c) Talet 54790 kan ha fyra eller fem gällande siffror eftersom nollor i slutet av ett heltal kan vara gällande. Det får man avgöra från fall till fall.
d) Eftersom nollor i början av ett tal inte är gällande har talet 0,034 endast två gällande siffror
Överslagsräkning
Överslagsräkning handlar egentligen bara om att göra det lätt för sig t.ex. då man använder huvudräkning och man ska räkna med tal där man måste hålla reda på decimaler och liknande. Som exempel kan man ta då man är och handlar.
Ola går till Konsum för att handla lite frukt. På handelslistan har han skrivit 2 bananer, 5 äpplen, 3 apelsiner och 4 päron. När han väger frukterna får han följande prisuppgifter:
2 bananer 4,40 kr
5 äpplen 11,65 kr
3 apelsiner 7,50 kr
4 päron 9,30 kr.
Räcker de 40 kr Ola har tagit med sig?
För att snabbt och enkelt räkna ut detta så kan Ola använda sig av överslagsräkning, vilket helt enkelt innebär att han avrundar decimaltalen till närmaste heltal.
4,40 –> 4 kr
11,65 –> 12 kr
7,50 –> 8 kr
9,30 –> 9 kr
Summan enligt överslagsräkningen blir:
Summan enligt de exakta priserna blir:
Som ni ser så räcker Olas pengar och det gick att räkna ut på ett ganska så simpelt sätt.
Avrunda rätt
Det finns vissa regler som säger om man ska avrunda ett tal uppåt eller nedåt.
Beroende på vilket platsvärde du ska avrunda till så tittar du på siffran närmast till höger om den platsen. Ska du t.ex. avrunda till närmaste tiotal så tittar du på entalssiffran för att avgöra om du ska runda uppåt eller neråt. Ska du avrunda till närmaste tiondel så tittar du på hundradels-siffran för att avgöra om det blir uppåt eller neråt.
Är siffran du tittar på 1-4 så avrundas talet neråt.
Är siffran du tittar på 5-9 så avrundas talet uppåt.
a) Avrunda 1,5 till heltal
b) Avrunda 24 till tiotal
c) Avrunda 2,8743 till 2 decimaler
d) Avrunda 7990 till hundratal
a) När vi ska avrunda ett tal till heltal så innebär det att talet inte ska ha några decimaler längre. Vi kikar alltså på det tal som har platsvärdet “tiondel”. Talet är en femma, alltså ska vi runda uppåt. Ettan på entalsplatsen blir alltså en tvåa.
b) Vid avrundning till tiotal så ska vi avgöra vad det är för en siffra som ska stå på tiotalsplatsen, tal med mindre platsvärde blir till nollor. För att avgöra detta tittar vi alltså på vad det står för siffra på entalsplatsen. I 24 är det en fyra som är entalet. Det innebär att vi avrundar neråt och tvåan får stå kvar som tiotal.
c) Här ska vi avrunda talet så att det enbart har två decimaler kvar. Vi ska behålla tiondelen och hundradelen. Tusendelen är den som står direkt till höger om hundradelen så det blir siffran med det platsvärdet som avgör hur vi ska avrunda. Tusendelssiffran är i detta fall fyra, alltså avrundar vi nedåt och behåller sjuan på hundradelsplatsen.
d) Här ska vi avrunda till hundratal. Vi tittar på platsen för tiotal och ser att det är en nia vilket innebär att vi ska runda hundratalssiffran uppåt. Men hundratalssiffran är också en nia, och när den rundas upp till tio blir den en nolla samtidigt som vi ökar på med 1 på tusentalssiffran. Således blir
1 augusti 2010 @ 11:16
hej! en jättebra sida, den tar upp blandade saker som är bra att ha i bakhuvet, men jag förstår verkligen inte det där om “gällande siffror”. Jag har alltid tänkt att nollor i slutet av ett tal med decimaler kan man skippa, de förändrar ju inte talets “värde”, men att nollor i slutet av ett heltal är jätteviktiga, det är ju skillnad på 500 och 5. Har jag bara fått allt om bakfoten, eller har jag lärt mig fel?
8 augusti 2010 @ 20:19
Frågor som dessa hänvisar vi till forumet. Tack för feedbacken
20 augusti 2010 @ 15:28
Hej! En riktigt bra hemsida, den får mig att tillbaka på banan igen efter ett långt sommarlov! För mig var allt solklart utom “gällande siffror” förstår det fortfarande inte helt riktigt… Har samma problem som Erika.
Annars en hemskt bra hemsida!
4 oktober 2010 @ 20:40
hej !
kan ni förklara vad betyder detta
c) Talet 54790 kan ha fyra eller fem gällande siffror eftersom nollor i slutet av ett heltal kan vara gällande. Det får man avgöra från fall till fall.
d) Eftersom nollor i början av ett tal inte är gällande har talet 0,034 endast två gällande siffror
mvh
alkeldani
8 december 2010 @ 19:36
Hej
Faktiskt jättebra hemsida. Bra att jag hittade den här sidan, har förlorad min matte bok och imorgon väntar nationella provet på mig. tungg
3 februari 2011 @ 22:10
det är brå vi får veta många på den har sidan tack så mycket
23 januari 2012 @ 10:25
yes bra
6 mars 2012 @ 14:36
bra matte
25 april 2012 @ 7:46
En sida som förklara matematik på ett enkelt sätt! Gillar! Den fungerar till och med I skolan med ungdomarna I min klass!
25 april 2012 @ 8:55
Tack för att Du delar med Dig av denna länk…tänk om man hade haft tillgång till den när man var inne och läste matte på gymnasiet…?! Det gick ändå tack vare en otroligt pedagogisk lärare som själv hade arbetat sig fram på ett fantastiskt sätt till att bli lärare…jag kunde höra hans röst och hans härledningar inne i mitt dåvarande inte fullt så klara huvud …tala om härledning…:)
25 april 2012 @ 16:58
*skratt* ja, så fungerar härledning sannerligen! Tänk att jag i dag undervisar på gymnasiet – det hade jag inte räknat med för några år sedan =0)
10 maj 2012 @ 13:45
bra sida
10 maj 2012 @ 15:09
??
16 augusti 2012 @ 16:26
Man får mycket jälp av denna sida.Tack
16 augusti 2012 @ 22:52
Thanx for sharing ..
18 augusti 2012 @ 4:55
Va får man? -:)
25 oktober 2012 @ 15:25
ok
4 januari 2013 @ 2:36
Men nej
1 december 2015 @ 13:48
Bra!! ) Tack
) Tack
31 maj 2016 @ 16:55
tack bror
18 juni 2016 @ 12:37
hej Anna ,,jag behöver lite hjälp med Matte, jag har en prov i Augusti:::kan du det..jag bor i Uppsala