Matte B - Funktioner
Funktionslära
Symbolen f(x)
Ni har förmodligen sett den här symbolen någon gång förut. Det är ett annat sätt att skriva en funktion. y=2x-3 kan också skrivas f(x)=2x-3. Då vi vill veta värdet på funktionen så sätter vi in et värde på x. Om vi vill veta vad funktionen f(x)=2x-3 får för värde då x=4 så skriver vi så här:
f(4)=2*4-3=5
Vi kan givetvis använda flera beteckningar för en funktion, t.ex. g(x), p(x) etc. Variabeln, som är mest känd som x, kan också ha en annan beteckning, t.ex.
p(q)=4q+5.

Funktionen f ges av . Beräkna
a) b) c) d)
a)
b)
c)
d)
Svar: a) 6 b) 6 c) 1 d) -6
Definitionsmängd och värdemängd
Definitionsmängden är de värden som variabeln (x) i en funktion kan anta.
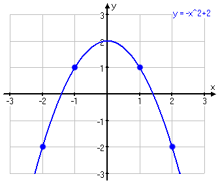
Värdemängden är de värden som funktionen (y) kan anta. Grafen nedanför har definitionsmängden och värdemängden
Nollställen
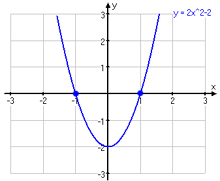
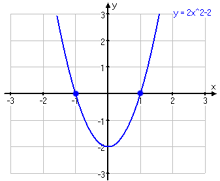
Nollställen kallas de ställen där funktionen f(x) antar värdet noll. Funktionen i grafen här nedanför har nollställena x=-1 och x=1.
Bestäm nollstället till den linjära funktionen f.
a) b)
a) Nollstället är alltså det ställe där funktionen är lika med noll f(x)=0 eller y=0.
Alltså sätter vi funktionen är lika med noll:
b)
Svar: a) b)
20 maj 2010 @ 21:43
Kunde du inte skriva så att man kunde kopiera till en uppsats
3 juni 2010 @ 8:05
Först och främst: Underbar sida! Jag blev så glad när jag hittade denna sammanställning. Skulle dock rekommendera att ni fixar stavfelet av matematik i inledningen till funktioner.
Skall försöka hinna med att gå igenom mer noggrant så småningom.
19 oktober 2010 @ 17:03
Väldigt bra sida för elever som behöver ett annat forum för att öva matematik. Tack!
23 oktober 2010 @ 23:14
Hej, jag sitter och försöker tänka ut hur det först är 1,5x-1=0 (på den sista uppgiften) och sen helt plötsligt blir det 1,5x=1. Vet att det kanske är jätte lätt om man bara tänker, men jag vet inte hur jag ska tänka så skulle vara jätte tacksam för hjälp.:)
25 oktober 2010 @ 20:36
Erik:
Ta +1 på båda sidor..
13 november 2010 @ 17:33
Erik:
tänk att du flyttar över -1 till högerledet. När man byter sida så byter man tecken. På så sätt så e 2x-4=0 samma sak som 2x=4
18 december 2010 @ 18:41
bra förklaring Elmer +++
3 februari 2011 @ 1:07
På exempel 1:
uppgift b)
Rätta mig om jag har fel men är inte lösningen
f(-2) = 10-(-2)^2 = 10+4 = 14
(Då -(-) alltid är = + [addition])
?
//Petter
3 februari 2011 @ 9:22
Hej Petter.
Jag rättar dig gärna.
f(-2) = 10-(-2)^2 => 10-(4) eftersom prioriteringsreglerna är att du ska lösa potenser före subtraktion. -2^2 =4
14 februari 2011 @ 12:48
Hej jag behöver hjälp med ett tal.
Funktionerna är definerade för de angivna x-värdena. Ange värdemängderna.
a). y=X^2-14,-3<X<3
b). y=x(10-2x), 0<x<5
9 mars 2011 @ 21:08
Är inte f(2)= 10-(2)^2 = 14? I o med att (-2)*(-2) = 4 som oxå är (-2)^2
9 mars 2011 @ 21:10
Nej det var bara jag som hade läst helt fel för att dom har inte skrivit () hehe
3 april 2011 @ 16:55
Hej hur ska jag räkna ut den här uppgiften:
låt f(x)= 3x-6 och g(x)= 8+x
a) f(x)-g(x)= 0
det är väl ungefär såna uppgifter som är uträknade ovan.. men jag förstår ändå inte.
Tack på förhand!
11 april 2011 @ 22:44
(3x-6)-(8+x) = 3x-6-8-x = 2x – 14
28 april 2011 @ 16:33
Lina
3x-6=8+x = 3x-x=8+6 = 2x=7 = x=7
12 maj 2011 @ 19:52
Varför anges definitionsmängden till mellan minus ett och plus ett ovan? Mig veterligen så är exemplet(y = 2x^2 – 2) definierat i alla värden på x…
16 maj 2011 @ 16:49
Hej! Jag undrar bara hur man räknar ut definitionsmängden och värdemängden?
20 februari 2012 @ 17:52
Bara att njuta av denna kunskap
20 februari 2012 @ 21:08
Du har faktiskt lov, du med!
17 augusti 2012 @ 12:25
mycket bra arbete:)).
16 januari 2013 @ 13:28
ajde
27 februari 2013 @ 12:54
lättförståeligt o bra!
7 oktober 2013 @ 12:36
Tack så mycket för hjälpen
13 april 2015 @ 15:36
jag håller fullständigt med gamle man