Matte B - Geometri
Likformighet
Likformighet
Då två figurer är likformiga så har de precis samma form, men är olika stora. Det vi då kan utnyttja är att deras motsvarande vinklar är lika stora och därmed är sidorna proportionella.
Likformiga månghörningar har
- motsvarande vinklar lika stora
- lika förhållanden mellan motsvarande sidor
Observera att trianglar är ett undantag/specialfall vad gäller reglerna för likformighet. De behöver bara uppfylla ett av kraven, närmare bestämt om det råder likformighet mellan trianglar om två av deras motsvarande vinklar är lika.
Likformiga trianglar har två motsvarande vinklar som är lika.
Då två figurer är likformiga och lika stora, dvs. kopior av varandra, så säger man att de är kongruenta.
Topptriangelsatsen och transversalsatsen
En parallelltransversal delar en triangel så att den får en topptriangel. Topptriangeln är likformig med den stora triangeln.
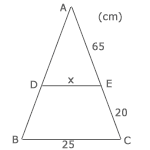Beräkna längden av DE i triangel ABC.
Om vi tittar på triangeln så ser vi att linjen DE är en parallelltransversal och därför är topptriangeln likformig med triangel ABC.
Det innebär att förhållandet mellan den stora triangelns bas och den lilla triangelns bas är lika stort som förhållandet mellan den stora triangelns sida och den lilla triangelns sida. Förhållandet får vi genom att dela den lilla triangelns mått med den stora triangelns mått eller tvärtom.
Antag: Sidan DE är x cm.
Svar: Linjen DE är 19 cm lång.
Bisektrissatsen
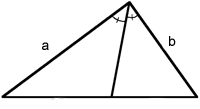En bisektris är en linje som dras rakt ut från ett hörn så att vinkeln i det hörnet delas i två lika stora vinklar. Då bisektrisen når motstående sida så delar bisektrisen den sidan i två sidor. Förhållandet mellan dessa sidor är detsamma som förhållandet mellan de två sidor (a och b) som går ut från hörnet bisektrisen delade mitt itu.
Om två sidor i en triangel har längderna a och b delar bisektrisen till vinkeln mellan dessa båda sidor och den tredje sidan i förhållandet a:b.
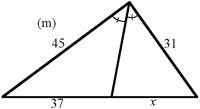Beräkna sträckan x.
Enligt bisektrissatsen så är förhållandet mellan sidan som är 45 m och sidan som är 31 m detsamma som förhållandet mellan 37 m och x m. 45 delat med 31 ska alltså få samma kvot som 37 delat med x. På så vis kan vi sätta upp en ekvation där vi kan lösa ut x:
Svar: x = 25 meter.
Areaskala och volymskala
Areaskalan förklaras under geometri i Matte A.
Volymskalan fungerar nästan på samma sätt som areaskalan, men här måste man ta skalan upphöjt till tre. Volymens enhet benämns ju som bekant i kubik-meter, -cm etc, alltså 3.
Längdsakala:
Areaskala:
Volymskala:
17 maj 2010 @ 22:03
Det här var ju kanonbra, precis vad jag letade efter, tack så mycket!
1 mars 2011 @ 22:31
Den här sidan är ju bara för bra! Har prov imorrn och jag tror faktiskt att jag fattar lite mer av all likformighet nu
15 maj 2011 @ 18:11
denna sida är ju förbra för att vara sann, vår mattelärare är inte den bästa men tack vare denna sidan känner jag att jag kmr klara provet mycket bättre!
21 maj 2011 @ 17:52
Vad för användning har jag utav att veta vad paralleltransversalen är?
Borde stå lite mer om i vilka tillfällen som man kan tänkas använda detta. Annars – super!
16 september 2012 @ 19:31
Förhållandet 2:1 ger kvoten 2/3, dela in sträckan AB I 3 lika stora delar.
Förhållandet 3:2 ger kvoten 3/5 på liknande sätt (dela I fem delar).
Någon som begriper hur man får 2:1 till kvoten 2/3?