Matte B - Linjära samband
Ekvationssystem
Här nedan ser vi ett så kallat ekvationssystem. Det är två ekvationer och “klammern” är till för att visa att y har samma värde.
Om man tittar på ekvationerna var för sig så ser man att de kan ha oändligt många lösningar, exempel på dessa ser du nedan.
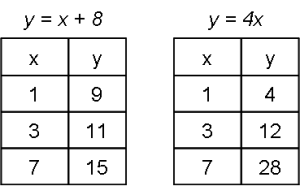
Grejen med ekvationssystem är att man bestämmer de ingående ekvationernas gemensamma lösning. Alltså det finns ett visst värde på x som funkar som lösning för båda ekvationerna och båda ekvationerna har då samma y-värde. Detta illustreras tydligt i en graf som vi ska kika på nedan.
Vi kan lösa ekvationssystemen på två sätt; algebraiskt eller grafiskt. Båda sätten är relativt enkla.
Grafisk lösning
En grafisk lösning av ekvationssystem bygger helt enkelt på att man bestämmer skärningspunkten mellan linjerna med de två ekvationerna. Det är koordinaterna i skärningspunkten som utgör lösningen till ekvationssystemet.
(Detta exempel är hämtat ur Gleerups Delta Matematik kurs A och B.)
Lös ekvationssystemet grafiskt.
Rita upp de båda linjerna antingen på ett papper eller i miniräknaren.
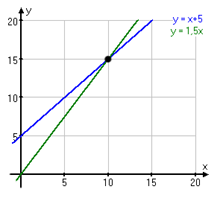
Linjerna har ekvationerna respektive . Skärningspunkten mellan linjerna har koordinaterna x=10 och y=15, vilket innebär att lösningen till systemet är x=10 och y=15.
Svar: x=10 och y=15.
Algebraisk lösning
Detta sätt att lösa ekvationssystem kan ibland vara att föredra eftersom det ger ett exakt värde på lösningen och kan även vara enklare att genomföra.
Lös ekvationsystemet
Sätt båda y-värdena lika med varandra.
För att få fram y så sätter vi in bara in x-värdet i en utav ekvationerna.
Insättning ger:
Svar: Lösningen är
Algebraisk lösning – Substitutionsmetoden
Denna metod bygger på att vi löser ut en variabel, antingen x eller y, i den ena ekvationen och ersätter (substituerar) den variabeln i den andra ekvationen med det uttryck man får. Därefter kan vi lösa ekvationen.
Om vi t.ex. löst ut x så måste vi sedan sätta in x-värdet i en av ekvationerna för att kunna räkna ut y-värdet.
Lös ekvationssytemet
Vi löser ut y i den första ekvationen…
…och ersätter y i den andra ekvationen med det uttryck vi fick fram:
Nu när vi vet vad x har för värde så kan vi också beräkna värdet på y:
Svar: Lösningen är
Algebraisk lösning – Additionsmetoden
Additionsmetoden är ett alternativ till substitutionsmetoden och är lämplig att använda när man inte kan lösa ut en variabel på ett enkelt sätt. Additionsmetoden bygger på att vi:
- ser till att en av variablerna (y eller x) i båda ekvationerna har ett tal framför sig (koefficient) som i ena ekvationen är motsatt tal till det i den andra ekvationen t.ex. -6y och +6y eller -2x och +2x. Detta ordnas genom att man multiplicerar den ena eller båda ekvationerna med lämpliga tal så att man får detta utseende (se exempel nedan).
- adderar därefter de båda vänsterleden och de båda högerleden med varandra och sätter dem sedan lika med varandra. Vi har då skapat en ekvation med en variabel som vi kan lösa.
- Lösningen på ekvationen t.ex. om vi fått ut y-värdet, sätter vi in i en av ekvationerna för att beräkna x-värdet.
Lös ekvationssytemet
Här ser vi att vi kan skippa första steget med multiplikation eftersom vi redan har en variabel som i en av ekvationerna är den motsatta mot den i den andra ekvationen, nämligen +y och -y. Vi kan genast gå över till att addera de båda ekvationerna och ser då att y-termerna försvinner och därmed har vi skapat en ekvation där vi kan lösa ut x.
För att sedan få fram y-värdet så sätter vi in x-värdet i en utav ekvationerna:
Svar: Lösningen är
Lös ekvationssytemet
Här krävs det att vi utför multiplikation innan vi kan addera vänster- respektive högerleden. Vi multiplicerar den första ekvationen med 3 och den andra med -2 för att koefficienterna hos x-termerna ska bli motsatta tal och därmed försvinna när vi lägger ihop vänsterleden och högerleden. Att vi väljer x är enbart slumpen, man skulle lika gärna kunna utföra en multiplikation som gör att y försvinner vid addering.
Vi adderar vänsterleden respektive högerleden och löser ekvationen.
Sätt in y=1 i en av ekvationerna för att ta reda på x-värdet:
Svar:
16 maj 2010 @ 21:16
I exempel 5 har Ni skrivit följande:
2x – y = 7 -> y = 2x + 7
Detta ska, enligt min mening, vara följande:
2x – y = 7 -> y = 2x – 7
(Endast för att det inte ska bli något missförstånd för övriga läsande)
16 maj 2010 @ 21:31
Tack för att du påpekade felet. Måste varit ett slarvfel eftersom det stod rätt på övriga ställen i exemplet.
24 maj 2010 @ 16:03
Går additionsmetoden och substitutionsmetoden lika bra att använda till samma tal? Och finns det något speciellt tillfälle då endast ena metoden ger rätt svar, eller går att använda, och den andra inte?
30 maj 2010 @ 2:33
Substitutionsmetoden funkar alltid, den är hundraprocentig. Det finns tillfällen då additionsmetoden ej fungerar, men generellt sätt så ska båda metoderna fungera på samma tal.
21 oktober 2010 @ 17:49
Jag förstår inte syftet med substitutionsmodellen..
5 november 2010 @ 15:19
substitutionsmodellen verkar bara extremt krånglig.
Dock fattar jag inte hur man ska veta vilket tal man ska multiplicera med då det är nödvändigt i additionsmodellen.
Exempel 4; hur vet jag att det jag ska multiplicera med är just 3 och -2?
6 november 2010 @ 16:35
Jag lovar att substitutionsmodellen blir den du kommer använda när uttrycken blir krångligare

I exempel 4 så tar vi just gånger 3 i första, och gånger -2 i andra: Bara för att vi ska få två ekvationer som man kan “addera ihop så att alla termer med x försvinner”. I vårt exempel tar vi 3 och -2 för att få 6x och -6x som svar. Adderar man ihop 6x och -6x så får vi noll.
Vi hade lika gärna kunnat tagit 6 och -4. Då hade vi fått 12x och -12x, vilket också blir noll när man adderar ihop
8 november 2010 @ 19:13
Tjennare! Jo jag undrar: Hur får ni x=6x-21+1 -5x=-20 ? Vad får man -5x ifrån?
13 november 2010 @ 17:37
@William:
Flytta alla X till vänster och siffror till höger så får du se.
24 mars 2011 @ 15:51
Hur räknar jag ut detta tal, det är ett ekvationssystem som ska lösas grafiskt
Y=3-x
Y=3x-1
24 mars 2011 @ 16:07
Det är den översta som jag inte kan rita upp, hittar inget m värde
24 mars 2011 @ 20:11
Hur räknar jag ut 2x-3y=11
y=2x/3+2
Med additionsmetoden?
Btw linda m-värdet är 3
25 oktober 2011 @ 14:35
Hej jag undrar hur man räknar ut det här ekvations systemet med hjälp av substionsmetoden: ( första ekvationen ) y-x=2
( andra ekvationen) 2x+y=8
25 januari 2012 @ 16:56
Ja, alltså…….
25 januari 2012 @ 16:56
Ja, alltså…….
25 januari 2012 @ 17:47
Haha. Fy f*n
28 januari 2012 @ 9:02
JAg skulle vilja veta hur man gör om man har x & y och ska ställa upp ekvationssystemet! känner mig helt lost..:s
31 januari 2012 @ 12:06
Jag föredrar additionsmetoden. Kolla exempel 3
1 mars 2012 @ 18:26
tack så mycket för hjälp
13 maj 2012 @ 15:51
Tobias Nyholm Det kallas faktist för subtitutions metod
13 maj 2012 @ 21:06
Marven Toma Det beror på vad man menar. I detta fall menar jag det jag skriver. Läs mer på denna sida så ser du att det finns något som heter både additionsmetoden och substitutmetoden.
18 maj 2012 @ 11:47
Tobias, Subtitutionsmetoden är när man ersätter antingen x eller y (eller z) termen vilket man gör i exempel 3. Alltså kallas det substitutionsmetoden.
18 maj 2012 @ 12:33
Jo tack jag vet. Jag skrev denna sida. I min kommentar från januari 31 så borde jag såklart referera till exempel 4. Typo av mig.
31 december 2012 @ 21:29
[...] My Academy ( matteguiden.se – linjära samband [...]
21 februari 2013 @ 20:41
bra förklarning… tack
27 februari 2013 @ 9:22
Behöver lite hjälp med ekvationsystemet (1) 3x+4y=22 (2) 2x+3y=17 !!!
!!!
såå krångliiigtt
17 april 2013 @ 16:51
Har ni lite hjälp för en. 7 som just har börjat med algebraiskt räkning???
17 april 2013 @ 17:31
Matte? Har du bytt bana? Vad gör du nu för tiden?
7 maj 2013 @ 10:48
kan man använda vilken metod som helst till alla lösningar eller måste man kunna alla
19 maj 2016 @ 23:46
X= -2 och y= 7