Matte B - Linjära samband
En linjes ekvation
k-form
Det är dags att lära sig hur man skriver upp en ekvation för en linje. Denna ekvation sägs vara skriven i k-form.
y = kx + m är en linjes ekvation i k-form. k är linjens riktningskoefficient och m är y-koordinaten för linjens skärning med y-axeln.
En rät linje skär y-axeln i punkten och har riktningskoefficienten 2. Vilket samband gäller mellan koordinaterna för en godtycklig punkt på linjen?
Vi sätter in de värden vi har i formeln för k:
är alltså ekvationen och sambandet för linjen.
Svar: Sambandet mellan x- och y-koordinaterna är .
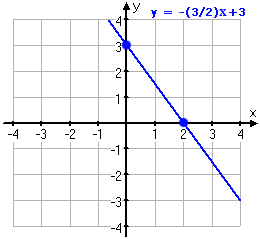
Rita linjen med ekvationen .
Då vi vet att m=3 så kan vi också säga att linjen går igenom punkten , stället där linjen skär y-axeln.
Om vi sedan går 2 steg åt höger och sedan 3 steg neråt så får vi en ny punkt på linjen. Därefter är det bara att dra en linje genom de båda punkterna.
Enpunktsformeln
Om vi vill bestämma en linjes ekvation i k-form och bara har riktningskoefficienten och en punkt given så kan vi använda oss av enpunktsformeln.
där vi vet värdet på k och punkten
Exemplet finns även som videoundervisning >>
En linje har riktningskoefficienten 1,5 och går genom punkten .
Bestäm linjens ekvation i k-form. Vi sätter in de värden vi har i formeln .
Svar: Linjens ekvation är .
En linje genom två punkter
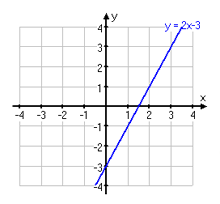En rät linje passerar genom punkterna och . Bestäm ekvationen för linjen.
Först räknar vi ut k.
För att räkna ut m så sätter vi in en av punkterna i ekvationen .
Ex. punkten
Detta ger oss ekvationen .
Svar: Linjens ekvation är .
Allmän form
Då vi skriver en ekvation för en linje i allmän form så skriver vi helt enkelt om ekvationen så att vi får 0 på höger sida.
Skriv ekvationerna och på allmän form.
Flytta över alla termer på vänstersidan och skriv konstanten sist i VL:
Flytta över alla termer på vänstersidan och skriv konstanten sist i VL:
För att få bort nämnarna så kan vi multiplicera alla tal med 15. 15 är det minsta talet som både kan delas med 3 och 5.
15 delas med 5 och kvar blir 3·4. 15 delas med 3 och kvar blir 5·1.
Svar: och
Varje ekvation på formen Ax+By+C=0, där A, B och C är givna tal och B ≠ 0, kan skrivas i formen y = kx + m och är därför ekvationen för en rät linje.
Då vi ska rita linjer i allmän form så är det ofta bra att bestämma skärningspunkterna med koordinataxlarna.
Rita linjen med ekvationen och skriv ekvationen på k-form.
För att kunna rita upp linjen behöver vi 2 koordinater. Förslagsvis kan vi välja koordinaten där x=0 och koordinaten där y=0. Om du sätter att x=0 så kan du lösa ut vad y har för värde i den punkten och tvärtom:
x=0 ger
y=0 ger
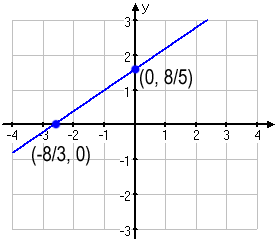Nu har vi räknat ut koordinaterna för de två punkter där linjen skär koordinataxlarna, nämligen punkterna och . Då återstår det bara att pricka in de två punkterna i koordinatsystemet och dra en linje genom dem.
Vi skulle även skriva om ekvationen i k-form:
Svar:
Parallella linjer
Två linjer är parallella om dem har samma riktningskoefficient eller båda är parallella med y-axeln.
Bestäm konstanten a i ekvationen så att motsvarande linje är parallell med linjen .
Vi skriver först om dem båda ekvationerna i k-form.
och
Då två linjer är parallella så har de båda samma k-värde. I och med det kan vi sätta respektive ekvations uttryck för k att de är lika med varandra:
På så vis har vi fått en ekvation där vi kan räkna ut konstanten a.
Då x finns i täljaren i både HL och VL så kan vi dividera bort det:
Flytta över fyran till andra sidan så att den hamnar i täljaren i HL:
Svar:
14 maj 2010 @ 0:44
I exempel 4 är första koordinaten fel – det står (0, 3) istället för (0, -3) vid typ två ställen.
14 maj 2010 @ 11:28
Tack Evy, nu är det felet åtgärdat.
17 maj 2010 @ 0:27
I exempel 2 står det m=2. Det ska vara m=3, och hela exemplet behöver då göras om.
17 maj 2010 @ 6:39
Sådär, nu ser exempel 2 bättre ut också. Tack Johan.
18 maj 2010 @ 1:02
i exempel 4, i meningen:För att räkna ut m så sätter vi en en av punkterna i ekvationen. ved menar du med “en en”? ska det vara: “in en” kanske?
18 maj 2010 @ 10:50
jo, självklart
29 juni 2010 @ 23:54
I exempel 2, står det y = (3/2) + 3 i stället för y = -3/2x + 3 . Hur så?
30 juni 2010 @ 0:39
Det är ett misstag. Ska rätta till texen i bilden nu.
2 juli 2010 @ 0:02
Exempel 6.
Om man löser ut K med hjälp av koordinaterna (0,8/5) och (-8/3,0) så blir K=-0,6. Där emot är 3/5=0,6. Hur kommer det sig?
Tack för en underbar sida, den är väldigt hjälpsam!
5 juli 2010 @ 6:53
Hej Sara.
Om man löser ut K med hjälp av koordinaterna (0,8/5) och (-8/3,0) så blir K=0.6, inte -0.6
28 juli 2010 @ 14:35
Nämnarna har nog glömts att ta bort på exempel 5, innan svaret räknats ut!
När 15 delas med 5 osv alltså.
28 juli 2010 @ 15:03
Hej N.
Det du säger stämmer. Jag har åtgärdat felet.
Tack!
9 augusti 2010 @ 2:02
Har nu fixat en del kvarvarande punkter efter att Tobias har varit och pillat. Jag har också städat lite i LaTeX:en, det skadar aldrig
11 september 2010 @ 15:24
Hej, i exempel 2 fattas ett minus tecken i ekvarionen precis ovanför grafen. Står y=(3/2)x+3, borde vara y=-(3/2)x+3
11 september 2010 @ 18:07
Hej Anders.
Nu är det fixat.
Om du fortfarande ser fel funktion så beror det på webbläsarens cache. Att uppdatera sidan borde göra susen.
20 oktober 2010 @ 16:25
Hej jag undrar hur räknar man ut k-värdet om det går en linje genom tre eller mer punkter? Tacksam för svar!
21 oktober 2010 @ 17:30
Anna:
Om alla punkter ligger på samma linje så är det ju bara välja två punkter. lutningen är samma över hela linjen.
7 februari 2011 @ 18:46
hej jag har ett matte tal som jag inte fattar riktigt.
ange en ekvation för linjen genom (3,6) då k=5
snälla hjälp mig
10 februari 2011 @ 23:13
Du har råkat skriva till “,5″ efter ettan i exempel 3.
11 februari 2011 @ 6:59
@niklas:
Hej. Nej exempel 3 är rätt.
15 mars 2011 @ 19:34
i exempel 3 så fattar jag inte de två sista uträkningarna,
y-2=1,5x-1,5 –> y=1,5x + 0.5 jag begriper inte hur 2 försvan och hur + 0.5 uppstod.
Snälla hjälp mig
16 mars 2011 @ 21:05
Det är så man räknar i ekvationer. Vi har tagit +2 i både vänster och höger led
26 april 2011 @ 22:35
I exempel 6 förstår jag inte varför 3x/3 = -8/3 y = -8/3. Ska det inte vara x = -8/3?
25 juli 2011 @ 12:25
I Ex:6 finns följande ekvationsberäkning
-5y+8 = 0
-5y = 8
om man flyttar över en konstant ska man väl byta från + till – ?
Dvs:
-5y+8 = 0
-5y = -8
25 juli 2011 @ 12:32
Rättelse:
I ert exempel blir
-5y+8=0
5y=8
Samtidigt som
3x+8=0
3x=-8
Finns det alltså något samband med att -5y blir positiv 5y och +8 förblir +8 när den flyttas över?
3 augusti 2011 @ 12:09
Nej inte direkt på det sättet du får det att låta. I ekvationen med 5y så har vi helt enkelt tagit +5y i båda led. Man måste inte nödvändigtvis flytta över konstanterna, man kan lika gärna flytta runt alla x och y mellan höger och vänster led.
7 december 2011 @ 14:33
Hej!
Du har rätt Joar att det ska vara x=-8/3 och inte y=-8/3, annars blir det två y koordinater istället för en y- och en x koordinat.
Hälsar
18 januari 2012 @ 11:30
Jag fattar inte riktigt Exempel 2:
“Om vi sedan går 2 steg åt höger och sedan 3 steg neråt så får vi en ny punkt på linjen.”
Varför går man just 2 höger/3 neråt? Har det med -(2/3)x i ekvationen att göra?
17 februari 2012 @ 9:37
kalas för elever som behöver ytterligare förklaring
20 februari 2012 @ 19:42
fuck
10 september 2012 @ 17:45
Under exempel 6 så ska det inte vara y = -8/3 utan det skall stå x = -8/3 eftersom y = 0 i den punkten
10 september 2012 @ 18:06
i exempel 7s beskrivnings så står det "Bestäm konstanten a i ekvationen så att motsvarande linje är parallell med linjen ." Men de glömde skriva in den sista linjens ekvation som är " X + 5Y + 1 = 0 "
15 november 2012 @ 16:44
Kurvan y=x2+A, där A är en konstant, går genom punkten(2;7). Bestäm ekvationen (på formen Y=kx+m) för en tangent till kurvan i punkten(2;7).
hur att lösa det här,, kan någon detta?
3 december 2012 @ 22:06
då vi ersätta (2,7) i ekvation så fick vi 7= 2.2 +A
A = 7-4 =3
y= 2x + 3
1 mars 2013 @ 20:30
Hej har ett Y som är 7 och ett ett X som är 2. Hur räknar man ut K? K=Y2-Y1/X2-X1. Problemet är att man har ett X och ett Y. Går formeln att använda eller måste man byta formeln? Kan inte få ut mer X eller Y på grund av tre mätningar som jag har tagit ut medelvärdet på att fått en punkt för X och en punkt för Y. Har inte linjen och det är den jag vill rita in tillsist.
2 mars 2013 @ 13:59
Jag var sjuk på den lektionen.