Matte B - Linjära samband
En linjes lutning
Vi kan illustrera olika linjära samband mellan två variabler i ett koordinatsystem genom att rita en rät linje. Då vi beskriver en rät linje i ett koordinatsystem så kan det vara bra att studera linjens lutning.
Först ska vi definiera när en linje lutar uppåt respektive neråt. Vi tittar helt enkelt från vänster till höger och där kan linjen alltså luta uppåt eller neråt.
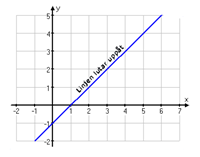
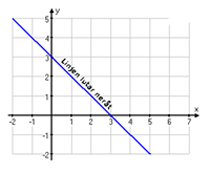
Det tal som bestämmer hur mycket linjen lutar kallas för linjens riktingskoefficient. Den berättar hur stor ändring det blir i y-led då man tar ett steg åt höger i x-led. Då vi flyttar oss ett steg åt höger på x-axeln och sedan rör oss uppåt i y-led för att fortfarande följa linjen, så är riktningskoefficienten positiv. Rör vi oss istället neråt för att följa linjen så är den negativ.
I enkla fall så behöver vi bara räkna rutorna i koordinatsystemet för att beräkna riktningskoefficienten.
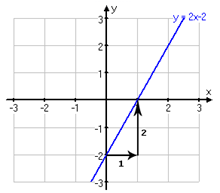
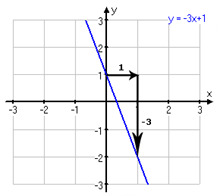
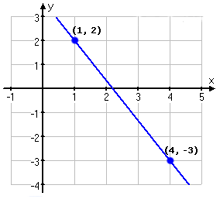
Ett steg åt höger, två steg uppåt. Riktningskoefficienten är 2.
Ett steg åt höger, tre steg nedåt. Riktningskoefficienten är -3.
Däremot så går det inte alltid att bestämma riktningskoefficienten genom att räkna rutor. Därför finns det en formel vi kan använda oss av då vi vet två punkter där linjen passerar i koordinatsystemet.
Riktningskoefficienten k för en linje kan beräknas genom
med hjälp av punkterna och som linjen går genom.
Bestäm riktningskoefficienten för den linje som går genom punkterna och
Notera att det inte spelar någon roll vilken punkt du börjar med:
12 maj 2011 @ 16:48
Lite svårt att förstå när det står y1=2y2=-3×1=1×2=4
Alltså utan mellanrum, ändra gärna det till
y1=2
y2=-3
x1=1
x2=4
16 maj 2011 @ 10:48
Tack så jättemycket! Förstod precis
27 maj 2011 @ 21:23
Tack till matteguiden, mycket bättre förklarat än i min mattebok. Tack även till John för förtydningen, fastnade också där.
28 maj 2011 @ 1:56
Håller verkligen med. Så jag lade till lite komman och mellanrum. Tack för inputen
24 augusti 2011 @ 17:09
Varför går -5 till 5 på första ? kan förstå andra förslaget när — blir plus..
1 september 2011 @ 16:14
Den var väldigt bra
31 oktober 2011 @ 22:17
Tack så mycket.!
16 november 2011 @ 13:23
Tusen tack, utmärkt förklarat
17 januari 2012 @ 13:21
roligt att alla i komentarsfältet tror att detta är rätt, bara jag som ser felen. hahaha
17 februari 2012 @ 9:46
hälsning till Ellen och Annelie
17 februari 2012 @ 10:50
För en gammal helklassiker är det mycket som är obegripligt i den matematiska världen…Men det kan ju finnas helklassiker som begriper mer än jag, förstås. F ö önskar vi Bobby och Yvonne en skön och avkopplande helg.
21 februari 2012 @ 13:42
TACK Hans! Även nu på sportlovet kliar skolan i fingrarna =yrkesskadan. Hoppas att även hos er skiner solen. Må gott
24 maj 2016 @ 13:11
Om man har en figur (t.ex en stjärna). Hur beräknar man åt vilket håll hela figuren lutar?