Matte C - Derivata
Definition av derivata
Definition av derivata
Man utläser f’(a) ”f prim a”.
Derivatan motsvarar tangentens riktningskoefficient i punkten P, alltså derivatan är då man tittar på lutningen i en viss punkt på en graf.
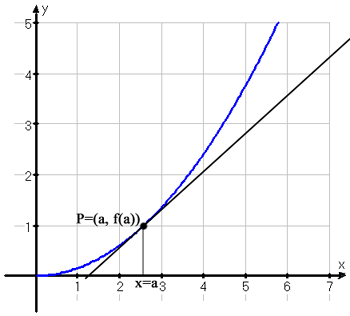
Då man drar en tangent till en funktion i en viss punkt så utgår man från punkten och ser sedan till att det raka strecket (tangenten) följer den ursprungliga grafen så mycket som möjligt på båda sidorna.
Då vi ska beräkna den så gör vi på följande sätt:
Beräkna f(3) och f(-2), exakt, då f(x) = 10x2
I båda dessa tal så gör vi följande för att räkna ut derivatan: Vi ersätter a i uttrycket
med 3 respektive -2 i de olika talen. Där det står f(a+h) ska man stoppa in funktionen som, i detta fall, är f(x)=10x2 och sedan ersätta x:et i funktionen med (a+h). I dessa två fall så är a satt till att var lika med 3 respektive -2 vilket vi då skriver in i parentesen.
Parentesen (a+h) behandlar vi alltså som om det vore x:et i funktionen. (Se rationella uttryck) Vi tar parentesen upphöjt till två och sedan gånger tio enligt funktionen f(x)=10x2. Siffran som vi sätter in på platsen där f(a) sitter, får vi lätt fram genom att sätta in talet 3 eller -2 i funktionen f(x)= 10x2. Detta ger oss:
Och
Lite längre fram i exemplena, då vi har 60h+10h2 eller -40h+10h2 kvar så faktoriserar vi det (kolla på innehållet i talen och bryt ut ett h) och får då ett h utanför parentesen vilket gör att vi kan dividera bort det med nämnaren. Redan från början har vi med hjälp av ”lim h –>0” visat att h går mot noll, och då vi tar bort uttrycket blir h=0 automatiskt och därmed försvinner det tal som multipliceras med nollan (h:et).
Derivata med annat skrivsätt
Derivatan kan även skrivas så här:
Hur vi använder den beteckningen kan ni se i exemplet nedan.
Låt f(x) = x2+1 och beräkna och skriv resultatet som en derivata
Förklaring av exemplet ovan:
Där det står f(x) sätter vi helt enkelt in uttrycket x2+1 eftersom det är x:et som står som variabel. Där det är a som står som variabel sätter vi in samma funktion, fast ersätter x:et med a:et. Efter lite uträkningar kommer vi fram till:
Om vi kikar i täljaren så ser vi att talet x2 – a2 ser ut som ett exempel på konjugatregeln >>. Då vet vi att man även kan skriva det på detta vis (se nedan) och till vår stora lycka har vi blivit av med nämnaren.
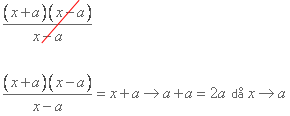
Om vi läser noga i början så ser vi att x går mot a, alltså omvandlas x till ett a och vi har slutligen 2a! Lätt som en plätt!
Deriveringsregler
Det finns massor av deriveringsregler. Många av dem används inte i den här kursen. Här hittar du en lista på dem vanligaste deriveringsreglerna.
22 juli 2010 @ 11:49
Hej!
Du som jag är så förstår jag inte varifrån 1:orna kommer i ex 2.
Tacksamm för hjälp!
22 juli 2010 @ 22:55
Det är klart du inte förstår det. Det är fel funktion. Jag har nu skrivit om funktionen i exempel 2. Nu är det mer klart var i från ettorna kommer.
12 februari 2011 @ 21:23
Väldigt bra sida Tobias, jag tackar
26 maj 2011 @ 18:12
Fråga angående första exemplet:
Du vill räkna ut f(3) och f(-2), och börjar direkt med att räkna ut derivatan. Varför? Om du vill räkna ut f’(3) kan jag förstå det, men f(3)?
22 november 2011 @ 21:21
Derivera funktionen
y = e^0,5x + 2x^3 + 1/x^3 – µx + 4/µx + 4 +2^3x
µ = är ruten ur , hittade inte tecknet
Får det till
y’ = 0,5e^0,5x + 6×2 – 3/x^4 – 1/2µx – 2/x^3/2 + ln(2) * 2^3x
vet inte om det är rätt? Hjälp mig
14 februari 2012 @ 7:35
Om man har glömt innebörden av derivering. så är detta en utmärkt resurs.
12 juni 2012 @ 15:08
Underbar sida
8 oktober 2012 @ 13:19
HERRE GUD derivata är det roligaste jag vet. Nu vet jag vad jag ska spendera eftermiddag på!
2 juni 2015 @ 8:58
Jag älskar er webbsida!