Matte C - Funktionsstudier
Största och minsta värde
Först ska jag bara reda ut ett begrepp. Det som menas med en ”definierad” funktion är alltså den delen av funktionen som är uppritad, oftast är det ett intervall angivet.
Då fortsätter vi…
En funktion har alltid ett största och minsta värde förutsatt att den är deriverbar och har en definitionsmängd som är lika med ett intervall av typen Det största värdet finner man där funktionen har sitt lokala maximum, och det minsta där funktionen har sitt lokala minimum. Alltså, måste värdet finnas i de punkter där derivatan är noll eller i ändpunkterna på intervallet.
Då ska vi lära oss hur man räknar ut största och minsta värde i en funktion.
Bestäm största värdet M och minsta värdet m till funktionen f, om f ges av där
Vi börjar med att derivera uttrycket och räkna ut x.
ger:
Svar:
Att x var lika med 1,5 då derivatan var lika med 0 så säger det oss att denna punkt kan vara antingen en maximipunkt, en minimipunkt eller en terrasspunkt. För att kolla vilken sort det är så räknar vi ut derivatan för ett lägre x-värde än 1,5 och derivatan för ett högre x-värde än 1,5.
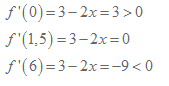
Resultatet kan vi sammanställa i en tabell som denna här nedan:

Den indikerar att punkten x=1,5 är en maximipunkt då lutningen innan punkten är positiv och lutningen efter punken är negativ – det går uppåt och sedan vänder det nedåt, något som diagrammet här nedan kan intyga:

Nu tar vi alltså och beräknar funktionens värde i intervallets ändpunkter x=0 och x=6 samt punkten där derivatan var lika med noll, x=1,5.


Av detta kan vi nu utläsa att det minsta värdet m är -18 och största värdet M är 2,25.
16 januari 2011 @ 17:30
I exempel 1 verkar uträkningen ha försvunnit.
16 januari 2011 @ 19:43
Jag har inga problem att se den. Har du javascript aktiverat? Tillåter du Ajax?