Matte C - Polynomfunktioner

Andragradspolynom

Skriv ut

Andragradspolynom

De två vanligaste och enklaste andragradspolynomer är y=x² och y=-x². Då man adderar ett positivt eller ett negativt tal till dessa funktioner så vet vi ju att de kommer att förflytta sig i höjdled.

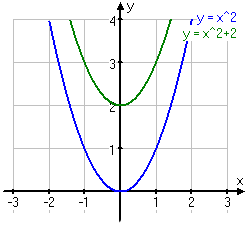
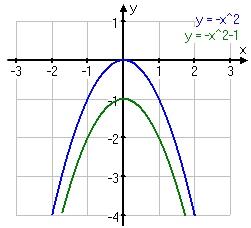
Dessa kurvor är symmetriska och följer i detta fall y-axeln, man säger då att y-axeln är en symmetrilinje till kurvorna.

Gillade du denna sida? Hjälp andra att hitta den!

Genom att trycka på länkarna här över så sprider du ordet om Matteguiden och hjälper oss att växa. På så sätt kan vi fortsätta att hjälpa besökare som behöver hjälp med matten.

1. Frida
   4 februari 2011 @ 9:16

   Kan ni hjälpa mig och min kompis lösa den här…

   Ett polynom av fjärde graden har fyra olika nollställen, -2,0,1 och 2. Dessutom vet vi att p(-1)=6. Skriv polynomet i faktoriserad form.

   Det vore jättesnällt om ni hjälpte oss.
   /Frida och Sandra

2. Simon
   20 november 2011 @ 13:37

   Väldigt sen hjälp frida och sandra, men jag hoppas kunna hjälpa några andra iaf.

   Så, om ditt tal sagt att det var en polynom av /andra/ graden och har två olika nollställen (ex. 2 och -3), vad hade ni svarat att dess faktoriserade form var? Jag hoppas ni hade svarat (x-2)(x+3)=0, för det borde det var.

   Varför inte göra samma sak för er fjärdegradare?

   Om dess nollställen är -2, 0, 1 och 2, borde inte polynomen se ut så här (x + 0)(x + 2)(x – 1)(x – 2) = 0?
   Den ger ju er alla nollställen ni vill ha.

   Iaf kan man faktorisera den där lite grann och komma fram till svaret (som jag hoppas är rätt annars har jag gjort bort mig rejält).

   x(x + 2)(x – 1)(x – 2) = 0

   x(x + 2)(x^2 – 3x + 2) = 0

   (x^2 + 2x)(x^2 – 3x + 2) = 0

   (x^4 – 3x^3 + 2x^2) + (2x^3 – 6x^2 + 4x) = 0

   x^4 – x^3 – 4x^2 + 4x = 0

3. Fanny
   12 januari 2012 @ 17:32

   Hej jag har lite problem men hur gör man när man räknar ut 6-(x-1)(x+2)(x+3) det ska förenklas?
   Och hur ska man tänka då det är 3 paranteser som ska multipliceras?
   Tack för hjälp fanny