Matte C - Potenser och logaritmer
Basen e
Basen e
Talet e är benämningen som vi har på det tal som man tar upphöjt med x för att få en kurva vars tangent i punkten (0,1) har riktningskoefficienten 1.
Om vi kikar på dessa tre nedanstående kurvor, så ser vi i första bilden att tangenten till kurvan y=2x i punkten (0,1) får en riktningskoefficient på ungefär 0,7. 
I andra bilden ser vi att riktningskoefficienten för tangenten till kurvan y=4x i punkten (0,1) blir ca 1,4.

I tredje bilden försöker vi hitta det tal som upphöjt till x blir en kurva vars tangent får riktningskoefficienten 1 i punkten (0,1). Detta tal måste enligt föregående bilder ligga någonstans mellan 2 och 4.

Efter vissa uträkningar, som jag inte har för avsikt att ta upp, så kommer man fram till att talet blir 2,718 28…osv, det är alltså detta tal som har betecknats med e.
Tangenten till kurvan y=ex i punkten (0,1) har alltså riktningskoefficienten 1. Det innebär även att om vi sätter att f(x)=ex så blir derivatan av det –> f´(0)=1.
f’(x)=ex -> f’(0)=e0=1
Att räkna med basen e
Följ dessa regler och det kommer att gå som en dans. Grekiska bokstaven Delta () betyder ”derivatan av”.
Där k är en konstant.
Beräkna derivatan:
a.)
b.)
c.)
Bestäm en ekvation för tangenten till kurvan i den punkt där kurvan skär y-axeln.
Då man kollar på derivatan för en kurva så får man fram lutningen i den specifika punkt man har valt. Tangenten är just den linje som visar lutningen i en specifik punkt på kurvan. Därför börjar vi med att derivera kurvans ekvation:
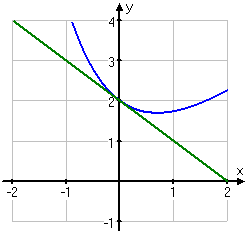
Om vi tittar på kurvan så ser vi att tangenten är dragen i punkten (0,2), x är noll och y är 2. För att få fram riktningskoefficienten så sätter vi in x-värdet i den deriverade ekvationen:
Räta linjens ekvation ser ju ut såhär:
och hittills har vi k = -1. m är ju som bekant värdet där kurvan skär y-axeln. m är alltså i detta fall 2.
Svar: Ekvationen för tangenten till kurvan är