Matte C - Potenser och logaritmer
Logaritmer
10-logaritmer

Exempel 1
Använd knappen ”log” på miniräknaren.
Skriv talet som en tiopotens. Ange exponenten med tre decimaler.
a.) 15,6
b.) 0,0256
Exempel 2
Lös ekvationen med tre gällande siffror:
a.)
b.)
Ekvationen ax=b
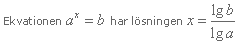
Exempel 3
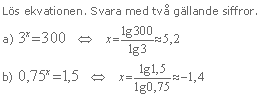
Naturliga logaritmer


Exempel 4
Lös ekvationen. Svara med tre gällande siffror.
a.)
b.)
12 april 2011 @ 6:14
kan ni hjälpa mig, tack
lg(0,5+20)+lg4=0,25.lgxUPHÖJ till 8
26 april 2011 @ 15:34
lg(o,5+20) + lg4 = lg 4(0,5+20) [log A + log B = log AB]
= lg (2 + 80) = lg 82
0,25 log x^8 = 8*0,25 log x = 2 log x = log x^2 [log x^y = y*log x]
ger:
log x^2 = log 82
x^2 = 82
roten ur så har du svaret. Borde stämma. Glöm inte att dubbelkolla ditt svar!
17 maj 2011 @ 16:42
Utan att använda sig av miniräknare… är Lg9 större eller mindre än 1? Motivera..
17 maj 2011 @ 17:31
x=Lg9. 10^x = 10^lg9 = 9. Lg9 måste alltså vara mindre än 1. Om det hade varit större skulle svarit bli >10.
19 maj 2011 @ 17:19
Kan ni snälla hjälpa mig?
2lnx=ln25 Hur löser man denna ekvation?
Tack!
19 maj 2011 @ 20:18
2lnx=ln25 -> lnx^2=ln25 -> x^2=25 -> x=25^½ d.v.s. roten ur 25 vilket är =5
26 maj 2011 @ 19:35
lös ut x ur
y=Ca^x
26 maj 2011 @ 22:06
y= Ca^x
lg(y) = lg(Ca^x)
lg(y) = x*lg(Ca)
lg(y)/lg(Ca) = x
30 maj 2011 @ 21:18
lös ut S ur
m = -2,512 x lg S
10 juni 2011 @ 13:20
m = -2,512*lg(S)
m/-2,512 = lg(S)
10^(m/-2,512) = S
28 juni 2011 @ 7:38
Kan ni hjälpa mig? Tack
1/2 1/3 1/4
2 . 2 . 2 =
27 september 2011 @ 18:32
Kan någon hjälpa mig med:
x^8 = 8
??
15 oktober 2011 @ 23:38
Hej, någon som kan detta?
5^2x+1=2^x-1
1 november 2011 @ 10:15
Hej någon som kan hjälpa med 70^1066 ?? hur ska jag tänka?
3 december 2011 @ 13:27
x^8 = 8
x = 8 ^(1/8)
14 mars 2012 @ 12:50
Om någon ser detta. Hur löser jag denna: om befolkningen I en by på glesbygden minskar med 3% per år. hur lång tid tar det tills befolkningen har minskat till hälften?
14 mars 2012 @ 12:50
Om någon ser detta. Hur löser jag denna: om befolkningen I en by på glesbygden minskar med 3% per år. hur lång tid tar det tills befolkningen har minskat till hälften?
14 mars 2012 @ 18:50
menar dom att den minskar samma antal som 3% innebar vid det första året, eller blir det tre procent på den "nya" befolkningen nästa år? Jag skulle ta ett hittepåtal, typ 1000 pers (för då är ju hälften 500) sen skulle jag räkna år för år hur många personer 3% är och hur lång tid det skulle ta att komma ner till 500pers. Och testa med en ny utgångssiffra om det blev fel, hahaha (långsamt med noga
Eller så kanske man kan räkna det baklänges bara. Har du inga siffror alls? Typ hur många som bor i byn NU eller hur många som KOMMEr att bo i byn när hälften försvunnit?
14 mars 2012 @ 18:57
ojsan, det kulle visst vara värsta fancy uträkningen :S Då är jag nog för glömd i huvudet för att kunna hjälpa :/
Jävligt irriterande, för ju mer jag tittar på exemplen börjar hjärnan vakna igen och fatta en del. Men jag skulle inte våga lita på att hjälpa dig, haha. Fast någongång skulle det vara kul att sitta med när du pluggar, friska upp minnet typ ^^
14 mars 2012 @ 23:11
Josephine Lundgren har klarat den uppgiften nu. Buhu för matte. nu har jag en ny jävel som jag för mitt liv inte kan lösa. 6upphöjd(x+2)=12upphöjdx
15 mars 2012 @ 12:04
Lyckades du fixa den? Jag glömde ringa upp när jag kom hem men bläddrade lite i min mattebok och kunde inte hitta hur man gjorde det. Svårt att förstå även om jag hade hittat det eftersom vi inte har kommit så långt ännu.
25 mars 2012 @ 15:22
hur löser man en ekvation av formen n^(x+y) = z? t ex 2^(x+3) = 11? vad gör jag med den där förbaskade trean I exponenten?
7 augusti 2012 @ 17:16
Hej, Jag heter Hassan Akbari , men jag bara gillar , ekvation Log,
27 april 2013 @ 13:56
hej hej jag heter samsom och jag tyckt logaritmer are bra
2 maj 2013 @ 18:34
sjukt dålig sida. 2/10
21 november 2014 @ 15:55
x*0,97^y=x/2
t ex 1000*0,97^y=500
0,97^y=0,5
y=lg0,5/lg0,97
y=22,757, y är lika med nästan 22 år 9 månader och 6,3 dagar
6 mars 2016 @ 14:01
OBS! Exempel 1 är felaktigt! Blanda inte in något Y där alls. Märkligt att ni tillåter sådan fel på en sådan här sida
27 april 2016 @ 15:20
Anne-Louise Buhr
6^((x+2) )=12^x
Tänkte börja med att skriva om ekvationen lite grann, från hemsidan http://www.matteguiden.se/matte-1/grunder/potenser/#Multiplicering-av-potenser
hämtar formeln: a^m * a^n = a^(m+n)
från vänster leden 6^((x+2) ) tänkte att a=6, m=x, n= 2, skriver om
6^((x+2) ) = 6^x * 6^2
http://www.matteguiden.se/matte-1/grunder/potenser/#Olika-baser
får formeln: (a*b)^n = (a^n) * ( b^n)
från höger leden 12^x får a=2 , b=6 och n=x , får då
(12)^x = (2*6)^x = 2^x * 6^x
Sätter man de två uttrycken med varandra får då
(6^x) * (6^2) = (2^x) * (6^x)
man kan sedan dividera både vänstra och högra leden med 6^x, det som blir kvar är
6^2 = 2^x
alltså längre upp på samma sida som vi är på så finns formeln:
Ekvationen a^x = b har lösningen x= lg(b) / lg(a)
tillämpar den, sätter b= 6^2=36 , a= 2 får då
x = (lg(36)) / (lg(2))
x = 5,169925001
sen kan man ju testa om svaret stämmer, sätter in svaret i ekvationen får då
vänster leden: 6^(5,169925001+2) = 379564,9529
höger leden 12^5,169925001= 379564,9525
nästan samma svar i den fjärde decimalen men annars låt säga att vänster leden = höger leden
Ett annat förslag på lösning är att skriva om både vänster och höger leden får samma bas, låt säga att vi skriver om dem med basen 10. Förmodligen kan man också skriva om med andra baser som talet e eller andra tal, men testade med basen 10.
Längre upp på samma hemsida får formeln: y=10^lg(y)
Skriver om
6 = (10)^(lg(6)) och 12 = 10^(lg(12))
Skriver ut ekvationen
6^((x+2) )=12^x som blir (10^lg(6) )^(x+2) = (10^lg(12) )^(x)
Ekvationen kan även skrivas om till
10^((lg(6)*(x+2)) = 10^((lg(12)*(x)))
Vi har samma bas alltså 10 men exponenterna är olika, för att lösa ekvationen måste exponenterna vara lika med varandra och löser ut x, sätter därför exponenterna lika med varandra får då:
lg(6)*(x+2) = lg(12)*(x)
på vänster leden multiplicerar in lg(6) i (x+2) får då lg(6)*(x+2) = (lg(6)*x )+( lg(6)*2)
exponenterna blir då
(lg(6)*x) + ( lg(6)*2) = lg(12)*x
subtraherar båda leden med lg(6)*x
(lg(6)*x) +( lg(6)*2) – (lg(6)*x) = ( lg(12)*x) – ( lg(6)*x)
får då
lg(6)*2 = lg(12)*x – lg(6)*x
i högra leden bryter ut x får
lg(6)*2 = x*(lg(12) – lg(6))
dividerar båda leden med (lg(12) – lg(6))
(lg(6)*2)/((lg(12)-lg(6))) = (x*(lg(12)-lg(6)))/((lg(12)-lg(6)))
får
x = (lg(6)*2)/((lg(12)-lg(6))) = 5,169925001
får samma svar som ovan om någonting är konstigt så får ni gärna rätta till, dem här förslagen är bara hur jag tror att man löser det.
27 april 2016 @ 15:37
2^(w+3)=11
Från längre upp på hemsidan hittar man formeln
Ekvationen a^ x = b har lösningen x = lg(b) / lg(a)
sätter a= 2 , b= 11 , x = w+3 får då
w+3 = lg(11)/ lg(2)
subtraherar 3 på båda sidorna får då
w = (lg(11)/ lg(2)) – 3 = 0,4594316186
testar svaret i ekvationen
2^(0,4594316186+3)= 11
svaret verkar stämma tror att man kan lösa det så här.