Matte C - Potenser och logaritmer
Potens- och logaritmfunktioner
Potensfunktioner
Potensfunktioner kallas sådana funktioner som har det typiska utseendet.
Här nedanför har vi ritat upp några sådana funktioner där värdet på C=1 och där positiva värden på a visas i den vänstra grafen och negativa värden på a visas i den högra grafen.
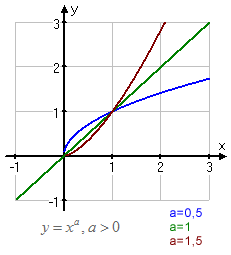
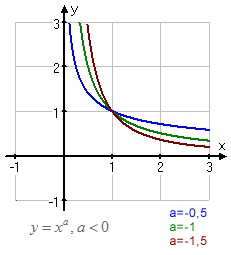
Då a är positivt så är f en växande funktion och då a är negativt så är den en avtagande funktion.
Lös olikheten grafiskt. Svara med två gällande siffror.
Eftersom vi ska lösa denna olikhet grafiskt så tar vi och plockar fram vår trogna grafräknare och knappar in de båda funktionerna y=x1,2 och y=3-x. Vi får då en graf som ser ut så här:
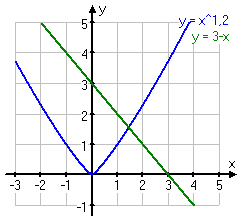
Lösningen, alltså värdet på x, finns där de båda kurvorna möter varandra. Klicka på 2nd-knappen och sedan knappen ”TRACE” vilket gör att vi får valet ”CALC” som står ovanför.

Här bläddrar vi nu ner till nr 5 ”intersect” som ska hjälpa oss att beräkna skärningspunkten, alltså var någonstans kurvorna korsar varandra. På skärmen får vi nu fram följande bild:
Här ovan ser vi nu att den kurva som är markerad är den som anges i övre vänstra hörnet, det är alltså på den som vår lille markör befinner sig på just nu. Vi ser också på skärmen att grafräknaren frågar efter den första kurva som är med och bildar skärningspunkten som ska beräknas. Den vill alltså att vi med vår markör ska markera den punkt på första kurvan som är så nära skärningspunkten som möjligt. Du förflyttar pricken längs kurvan med hjälp av höger och vänster pil.
När du tycker att du har passat in pricken med punkten där kurvorna möts så klickar du ”ENTER”. Och följaktligen får vi fram nästa skärmbild som du ser här nedanför:
Vi ser här att den kurva som är markerad nu är y=3-x och det är på den som vår markör nu är fäst. Grafräknaren frågar denna gång efter den andra kurvan som är med och bildar skärningspunkten. Vi flyttar alltså vår markör med höger och vänster pil och passar in den så bra som möjligt i mötespunkten.
När du känner dig nöjd, klicka ”Enter”. Det sista grafräknaren ber dig göra nu är att gissa var exakt skärningspunkten är. Så flytta runt markören tills du tycker du har träffat mitten och klicka än en gång ”Enter”:
Innan du ens har hunnit blinka så presenterar grafräknaren följande resultat:
Skärningspunkten mellan kurvorna y=x1,2 och y=3-x har koordinaterna (avrundat) x=1,4 och y=1,6.
Hur ska vi då svara? Eftersom detta är en olikhet så är x antingen större än eller mindre än 1,4, men hur vet vi det då? Jo, man kan antingen läsa ut detta grafiskt eller helt enkelt testa sitt svar genom beräkning.

Grafiska utläsningen: Om vi kollar på grafen ovan så ser vi att kurvan x1,2 är mindre än linjen 3-x ända fram till den punkt x=1,4 där de möts. Alltså, kurvan x1,2 har ett lägre y-värde än linjen 3-x ända fram till deras skärningspunkt. Då kurvan har passerat linjen så är det den som har större y-värde än linjen. Villkoret som olikheten x1,2 < 3-x anger är ju att kurvan x1,2 skulle vara mindre än linjen 3-x och det villkoret uppfyller den kurvan ända fram till precis innan punkten 1,4.
Alltså blir vårt svar att x < 1,4, för det är då olikheten är sann. x får inte vara lika med 1,4 för i den punkten har de båda graferna samma värde och det är ju inte det som olikheten talar om för oss eller hur?
Uträkningen: Om ni tycker att det är klurigt att läsa ut detta ur en graf så kan ni istället helt enkelt testa er lösning. Vi har två lösningar att välja mellan: x < 1,4 och x > 1,4.
För att testa om x är större än 1,4 är rätt så tar vi helt enkelt ett värde som är större än 1,4 t.ex. 1,5 och sätter in det i olikheten:
testas:
Som ni ser så är ju inte alls 1,63 mindre än 1,5, vilket innebär att denna lösning är fel.
Då testar vi istället x<1,4 och väljer då ett värde som är mindre än 1,4 t.ex. 1 och så sätter vi in det i olikheten:
testas:
Denna gång stämmer det då 1 faktiskt är mindre än 1,7, och därmed kan vi konstatera att svaret blir x < 1,4.
Denna uppgift är hämtad ur Gleerups Nya Delta Matematik kurs C.
För en rördiod beskrivs sambandet mellan strömmen i A (Ampere) och spänningen i u V (Volt) något förenklat av likheten:
Bestäm om strömmen är 0,020A när spänningen är 5,0V.
Först börjar vi med att skriva om uttrycket så att k, som vi ska räkna ut, hamnar ensamt på vänster sida. Sedan sätter vi in värdena för strömmen och spänningen och då kan vi sedan beräkna k hur lätt som helst. Efter att ha avrundat lite får vi svaret 0,0018.
Logaritmfunktioner
En logaritmfunktion är en funktion som antingen innehåller uttrycket lg eller ln. Vi ska titta lite närmare på dem så vi tar och ritar upp funktionerna f(x)=lg x och f(x)=ln x i ett koordinatsystem.
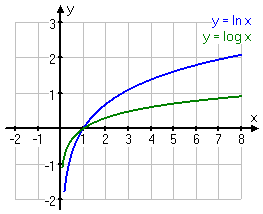
Nu när vi tittar på dessa två kurvor så kan vi dra följande slutsatser:
- Logaritmfunktioner är strängt växande
- Logaritmer är negativa då 0 < x < 1
- Logaritmen för talet 1 är 0, alltså då x=1 så är y=0
- Logaritmer är positiva då x>1
- Logaritmer för negativa tal finns inte, alltså grafen passerar aldrig x=0 och fortsätter mot de negativa värdena på x.
(Om ni testar att skriva in ln -1 eller log -1 på miniräknaren så kommer den att säga ifrån. Miniräknarens reaktion kommer dock att variera beroende på hur ni har den inställd. Är den inställd på att endast visa reella tal så kommer den att protestera mot att ni skriver en logaritm för ett negativt tal. Däremot är den inställd på att även visa imaginära tal så kommer ni att få ett sådant svar.)
Lös ekvationen/olikheten grafiskt och ange lösningen med två gällande siffror.
a.)
b.)
a)
Vi skriver in våra två funktioner y=lg x och y=5-x på grafräknaren.
Och får då en graf som ser ut så här:
Med hjälp av alternativet ”intersection” beräknar vi skärningspunkten och får då ett x-värde som avrundat blir x=4,4 och det är vår lösning på denna ekvation.
b)
Vi skriver in våra två funktioner y=ln(x-1) och y= x-3 på grafräknaren.
Vi får då fram en graf med detta utseende:
Då denna graf innehåller två skärningspunkter funktionerna emellan så innebär det att det finns två lösningar på denna olikhet. Vi börjar med att räkna ut båda skärningspunkterna med verktyget intersection och får då (avrundat) x=1,2 i första punkten och x=4,1 i andra punkten.
Första lösningen på denna olikhet har med vår första punkt att göra, x=1,2. Om vi tittar noga på grafen så ser i att kurvan ln(x-1) uppfyller villkoret att ha lägre y-värde än linjen x-3 innan den når punkten x=1,2. Alltså kan vi konstatera att x < 1,2 gör så att olikheten ln(x-1) < x-3 blir sann.
MEN, vi får inte missa den lilla detaljen. Notera i grafen att kurvan ln(x-1) får ett abrupt slut då den närmar sig x=1.
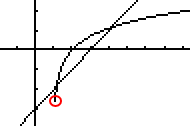
Om vi utgår från denna skärmbild så klickar vi på knappen 2nd och sedan knappen WINDOW för att komma åt det blå alternativet TBLSET. Du får då upp denna skärmbild, dock kan det stå helt andra värden beroende på vad du har gjort tidigare.
Fyll i de värden som du ser ovan: -1 och 5 och AUTO ggr 2.
Sedan klickar du återigen på 2nd och sedan på knappen GRAPH, vilket gör att vi kommer åt det blå alternativet TABLE. Och vi får då fram det här:
Här ser vi y-värdena för varje x-värde på de grafer som är uppritade. Y1 är vår kurva ln(x-1) och där x=1 så ser ni att det inte finns något sådant y-värde för den kurvan. Det existerar faktiskt inte några y-värden för något x-värde som är mindre än eller lika med 1.
Alltså kan vi nu lägga till denna detalj till vår första lösning och säga att olikheten uppfylls då x är större än 1 och mindre än 1,2: 1 < x 1,2.
Den andra lösningen får vi genom att nyttja x-värdet från vår andra skärningspunkt, nämligen x=4,1. Vi plockar åter fram vår graf:

Villkoret som ska uppfyllas var att kurvan ln(x-1) skulle ha lägre y-värden än linjen x-3. Det ser vi att den har efter punkten 4,1 och då blir alltså vår andra lösning att x är större än 4,1, x > 4,1.
Det slutgiltiga svaret på b-uppgiften är: 1<x<1,2 eller x > 1,4