Matte C - Rationella uttryck
Förenkling av rationella uttryck
Minsta gemensamma nämnare
Då vi ska förenkla summor av bråkuttryck så gäller det att hitta den minsta gemensamma nämnaren, mgn.
När den minsta gemensamma nämnaren (mgn) ska bestämmas tar man med varje faktor så många gånger som den finns i störst antal i någon nämnare.
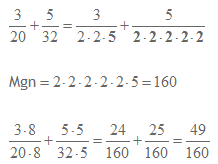
Vi delar upp nämnarna i deras olika faktorer, se ovan. Där ser vi att det finns två faktorer nämligen 2:an och 5:an. Det största antalet 2:or ser vi i det andra bråkets nämnare, alltså 5 stycken. Största antalet 5:or ser vi i första bråkets nämnare, alltså en 5:a. För att räkna ut mgn tar vi alltså och multiplicerar de 5 tvåorna med varandra och gångar sedan detta med 5:an. Mgn blir då lika med 160. För att våra två bråk ska få 160 som nämnare så multiplicerar vi dem med varsitt lämpligt tal.
Det första bråket behöver multipliceras med 8 (20*8=160) och det andra bråket behöver multipliceras med 5 (32*5=160). Täljarna ska också multipliceras med det tal som deras nämnare multipliceras med.
När bråken väl fått samma nämnare så är det bara att lägga ihop täljarna och där har vi svaret. Var noga med att du ska svara i den enklaste formen så kolla alltid ifall bråket går att förkorta. Dock är det inte så i detta fall.
Faktoruppdelning
Då man gör en faktoruppdelning så bryter man ut de gemensamma faktorerna som finns i talen. För att kunna se dem är det viktigt att man tittar på innehållet.
2 2 a är gemensamma faktorer, dvs man kan hitta dem i båda termerna. 2 2 a finns alla tre på båda sidorna av minuset – i vårt exempel.
Här är 2 2 2 b gemensamma faktorer, eftersom alla 4 finns på båda sidorna av “plusset”.
Gemensamma faktorer här är 2 2, eftersom båda måste finnas på båda sidorna av minuset här.
Har man riktigt tur så kan man även stöta på sådana tal som gör att man kan använda en utav de två kvadreringsreglerna eller konjugatregeln.
Första kvadreringsregeln:
Andra kvadreringsregeln:
Konjugatregeln:
Så här gör vi när vi delar upp ett uttryck i faktorer:
- Bryt först ut de faktorer som är gemensamma för alla termer.
- Om polynomet har två termer:
…kolla om du kan använda konjugatregeln. - Om polynomet har tre termer:
…kolla om du kan använda en utav kvadreringsreglerna.
Funktionssymboler
I exemplet nedan så ersätter vi helt enkelt x med det som står inuti parentesen hos f.
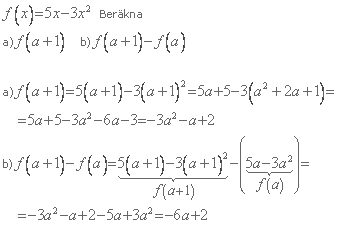
9 mars 2011 @ 11:52
Hej. Jag har lite problem med denna uppgift.
Man ska lösa denna rationella ekvation.
1/x + 1 = -3 / 2(x-1)
15 april 2013 @ 11:18
va?