Matte D - Integraler
Areaberäkningar
Arean av området mellan en funktionsgraf och x-axeln
Då vi ska räkna ut arean av ett område under en funktion i intervallet och som begränsas av x-axeln, så använder vi oss av följande formel:
Notera! Funktionen måste vara positiv i hela intervallet.
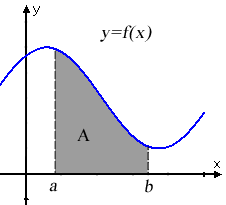
Om funktionen istället är negativ i hela intervallet så är arean istället lika med minus integralen över intervallet.
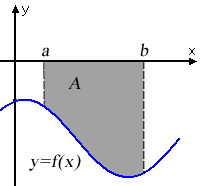
Beräkna arean av det markerade område där kurvan som begränsar området uppåt har ekvationen
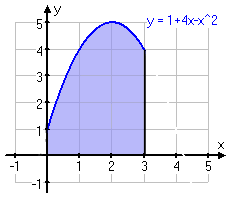
Jaha, kurvan är ju angiven så det vi behöver för att kunna beräkna arean är ju intervallet. I den vänstra bilden, som tillhör a-uppgiften, så ser vi ganska tydligt att den markerade arean börjar vid y-axeln, alltså där x=0. Den slutar sedan då x=3
Vi sätter alltså upp vår integral på följande vis:
Vi har skrivit att integralen ska beräknas i intervallet från 0 till 3, och funktionen som är angiven är den som det gäller. Så nu är det bara att beräkna integralen. Det första steget blir att omvandla vår funktion till en primitiv funktion:
Sådärja, då är det bara att börja räkna. Vi skriver ut vår primitiva funktion och ersätter x:en med den övre gränsen i intervallet, alltså trean. Därefter så skriver vi minus och sedan skriver vi ut den primitiva funktionen och ersätter denna gång x:en med den undre gränsen, alltså nollan. Vi får inte heller glömma att sätta dit parentesen runt den funktionen som vi subtraherar med!
Sedan är det bara att fortsätta räkna:
Arean för det markerade området är alltså 12 areaenheter, förkortat a.e.
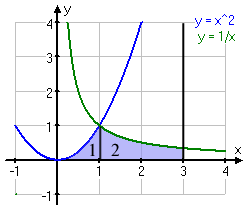
Beräkna arean av det området som begränsas av kurvorna y=x2 och y = 1/x, x-axeln och linjen x=3.
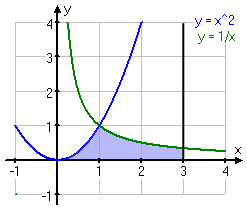
Området som vi ska beräkna arean av ser du här ovanför, det blåmarkerade området. Som du ser så sträcker sig området från x=0 till x=3. MEN, det finns två problem; det första är att kurvan 1/x inte har något värde för x=0. Det andra problemet är att kurvan x2 bara har areaområdet från x=0 till x=1.
För att kunna beräkna arean på detta område så måste vi dela upp den i förslagsvis två delar. Då man gör detta utgår man ifrån den punkt där kurvorna skär varandra. I detta tal är det relativt enkelt att konstatera att skärningspunkten är där x=1:
Hade man däremot inte kunnat lösa ut skärningspunkten grafiskt så går det även att räkna ut den hel enkelt genom att sätta de båda kurvorna lika med varandra:
Iaf, vår första areabit, nr 1, får följande uttryck:
Detta eftersom det är just x2-kurvan som området följer i intervallet 0 till 1. Vi beräknar alltså arean på det område under kurvan i intervallet 0 till 1.
Från punkten där x=1 och framåt till x=3 så är det kurvan 1/x som följs och därför får vi följande uttryck för dess area:
För att få fram den totala arean behöver vi alltså bara lägga ihop de båda uttrycken:
Vi skriver ut de båda primitiva funktionerna separat:
Sen är det bara att börja räkna:
Svar: Arean av området är 1.432 a.e. stort.
Arean av området mellan två funktionsgrafer
Då vi beräknar arean av ett visst område på en kurva så menar vi ju den yta som finns under kurvan, precis som i bilden här nedan:
Hur gör vi då när vi ska beräkna arean av det område som uppstår mellan två funktionsgrafer? (se de två bilder nedan)
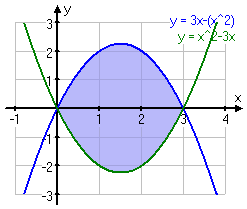
Om vi jämför dessa två bilder här nedan så ser vi att det stora blå området i vänster bild har begränsats av den undre kurvan till ett mindre område.
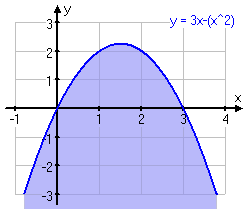
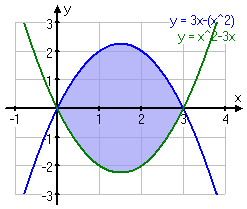
Den begränsas av den area som finns under vår undre kurva om vi beräknar den in samma intervall som den övre.
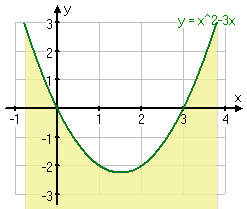
Som ni ser i den nedre bilden så tar delar av det gula området ut delar av det blå området vilket ger oss det begränsade området. Vi behöver inte bry oss om det gula på kanterna då de inte ingår i området. Områdets intervall är ju mellan de båda skärningspunkterna.
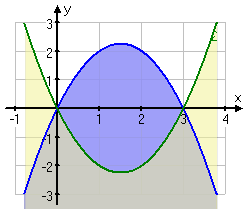
För att räkna ut arean på detta begränsade område så måste vi alltså ta arean av den övre funktionen minus arean av den undre funktionen. Med övre och undre kurvan menas kurvornas placeringar i koordinatsystemet. Intervallet bestäms för det mesta med hjälp av beräkningar på skärningspunkterna kurvorna emellan, om inget annat anges.
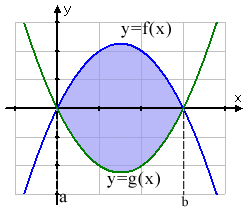
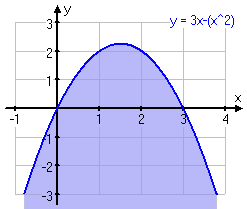
Beräkna arean av det område som begränsas av kurvorna
och
Innan vi ställer upp integralen, som hjälper oss att räkna ut arean av området, så måste vi ta reda på i vilket intervall det gäller. Det gör vi genom att beräkna x då y=1 alltså där kurvorna skär varandra.
För att lösa ut x så byter vi först ut tecknen så att x2 blir positivt, det underlättar då vi räknar. Sedan bryter vi ut x genom faktorisering och där kan vi då se att x antingen är 0 eller 2.
Tittar vi på grafen så ser det ju ut att stämma med skärningspunkterna.
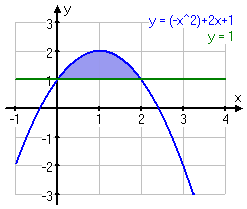
Nu kan vi alltså sätta upp vårt uttryck för area genom att ta integralen av den övre funktionen minus integralen av den undre funktionen:
Svaret blev till slut 4/3 a.e. Då man tar en integral minus en annan och det gäller samma intervall så kan man slå ihop uttrycken precis som vi gjorde här ovan. Som ni ser så tar ju +1 och -1 ut varandra och kvar blir –x2 och +2x som vi gör om till en primitiv funktion och sedan sätter in integrationsgränserna och räknar fram till 4/3 a.e.
29 maj 2010 @ 23:42
Hur avgör man vilken som är undre och övre funktion om man inte har kurvorna ritade??
30 maj 2010 @ 14:20
Du kan ta reda på vart kurvorna skär varandra genom g(x)=f(x). Om dem har två skärningspunkter x1 och x2. Testa en punkt p mellan x1 och x2. Om g(p)>f(p) då är g(x) den övre funktionen.
8 augusti 2010 @ 20:32
Generellt sätt så hänvisar vi frågor som denna till Forumet.
22 mars 2011 @ 12:43
I exempel 3 har det smugit sig in ett litet fel. Ni byter tecken för att det ska bli enklare att beräkna intervallet. Dock har ni glömt att byta tecken i högerledet.
22 mars 2011 @ 17:46
Absolut rätt, tack så mycket. Åtgärdat!
18 maj 2011 @ 22:14
Den här bilden finns med på sidan:
http://www.matteguiden.se/wp-content/plugins/php-image-cache/image.php?path=/uploads/2010/01/areaberakningar10.png
Den är lite missvisande då den visar att integralen beräknar arean under hela grafen, medan integralen egentligen beräknar arean mellan kurvan och x-axeln. Eller är jag helt ute och cyklar så här 10 timmar innan det nationella provet?
9 december 2012 @ 11:31
ofta?
15 december 2014 @ 9:37
Wuuut?!
27 december 2014 @ 12:48
tack sö mucket hitlyr