Matte D - Trigonometri i trianglar

Cosinussatsen

Skriv ut

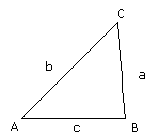
Jag hoppas att sinussatsen kändes ganska enkel och lättförståelig, den kommer att bli mycket användbar. Om vi nu istället skulle hamna i en sådan situation där triangelns alla sidor är kända men ingen vinkel, så kulle det dock ställa till lite problem. Den enkla lösningen på det hela är cosinussatsen, som även går att använda då vi vet två sidor och den mellanliggande vinkeln.

Tips!

Det underlättar om du först räknar ut motstående vinkel till den längsta sidan då du vet alla tre sidorna. Det gör du med hjälp av cosinussatsen. På det sättet får du direkt veta om vinkeln är spetsig eller trubbig. Om den är trubbig kan du så vet du att de övriga vinklarna är spetsiga, och då kan du alltså beräkna dessa med sinussatsen.

Gillade du denna sida? Hjälp andra att hitta den!

Genom att trycka på länkarna här över så sprider du ordet om Matteguiden och hjälper oss att växa. På så sätt kan vi fortsätta att hjälpa besökare som behöver hjälp med matten.

1. Jasmine
   18 maj 2010 @ 1:54

   Hej Matteguiden! Om man tittar på rad 2:
   42,25 = 154,25 – 152 cosA >> 112 = 152 cosA
   Jag undrar, om man flyttar över 154,25 till andra sidan då blir det ju: 42,25 – 154,25 = -112 (alltså blir svaret negativt inte positivt). Så man får -112 = -152 cosA
   Är det dumt? </
   Tack!

2. Jasmine
   18 maj 2010 @ 2:01

   Jag är kanske för noga men, ni bör rätta till sista delen av B-vinkel beräkningen. Det står:
   B = arccos 0,7 = 53,1 och skriva 0,6 istället.

3. Tobias
   18 maj 2010 @ 11:03

   Hej Jasmine.
   Rad 2 i exemplet är rätt. Om du flyttar över 154.25 som du tänker så får man som sagt -112 = -154 cosA . Om du då multiplicerar båda sidorna med -1 så får du 112 = 154 cosA. Så likheten stämmer.

   I beräkningen av vinkel B har vi gjort fel som du påpekade. Felet är nu åtgärdat.

   Tack för dina kommentarer.

4. Fredrik Boman
   8 december 2012 @ 20:26

   Lördagkvällen blev perfekt..