Matte D - Trigonometri i trianglar

Trubbiga vinklar

Skriv ut

Sinus och cosinus


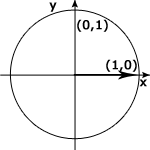
Enhetscirkeln är ritad i ett koordinatsystem och har sin medelpunkt i origo (0,0) och dess radie är en längdenhet. I cirkeln har vi ritat en visare som går från origo till punkten (1,0), den ligger alltså längs med x-axeln. De fyra olika rutorna kallas för första, andra, tredje och fjärde kvadranten.










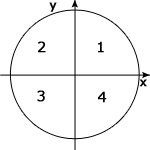
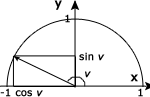
Vi vrider visaren moturs kring origo så att den bildar vinkeln v mot sitt ursprungsläge. Det relevanta här är vinklar mellan 0° och 180°.



Nu inför vi dessa definitioner:

är y-koordinaten i enhetscirkeln
är x-koordinaten i enhetscirkeln

Dessa definitioner stämmer väl överens med det vi har lärt oss innan. I figuren här ovan ser vi att det stämmer för spetsiga vinklar. Här är motstående kateten sin v och närliggande cos v medan hypotenusan är radien som alltså är 1. Det hela stämmer alltså överens med definitionerna för sin v och cos v i rätvinkliga trianglar



Gillade du denna sida? Hjälp andra att hitta den!

Genom att trycka på länkarna här över så sprider du ordet om Matteguiden och hjälper oss att växa. På så sätt kan vi fortsätta att hjälpa besökare som behöver hjälp med matten.



Tips! Få hjälp av en coach inom Trubbiga vinklar och andra utmaningar inom matematiken. Slå MyAcademy en signal på 08-506 655 10 eller maila på info@myacademy.se.

  1. Cecilia
    16 januari 2012 @ 18:27

    ”I figuren här ovan ser vi att det stämmer för spetsiga vinklar.” Menar ni inte trubbiga? Annars ser jag inte vilken vinkel ni menar.
    MVH