Matte D - Trigonometriska funktioner

Lös ekvationerna i intervallet

a) b) c)
Det är lättas att se lösningarna om vi ritar upp dem i enhetscirkeln

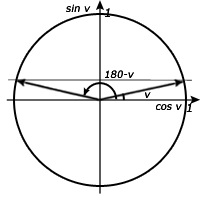
Lösning till a)
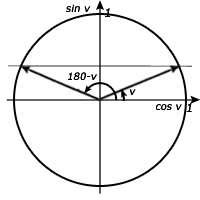
Som ni ser har två lösningar då samma punkt finns representerade på den andra sidan om y-axeln. Om vi knappar in på vår miniräknare får vi fram en vinkel. Den andra vinkeln är en så kallad supplementvinkel och formeln för att erhålla den är I detta fall får vi att
och

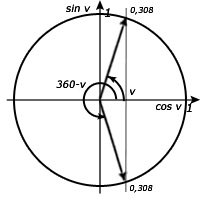
Lösning till b)
Räkningarna följer exakt dem för a.


Här ser vi att det finns två lösningar. För att nå supplement vinkeln för cosinus måste vi passera 2:a kvadranten och in i den 4:e kvadranten. Dessa två vinklar bildar tillsammans ett helt varv och vi måste subtrahera startvinkeln för att få fram den andra vinkeln (supplementvinkeln).

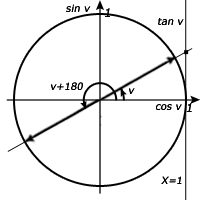
Lösning till c)


Som vi kan se är tangens lite speciell. Som vi kan se hamnar supplementvinkeln ett halvt varv på motsatt sida om vinkel ett. Därmed får vi reda på den andra vinkeln genom att addera 180 grader på den första vinkeln.

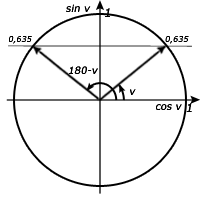
Lös ekvationen med en decimal

Första uppgiften lösen vi som vanligt. Vi låter miniräknaren bestämma värdet för v = arcsin 0,635 och sedan räknar vi ut supplementvinkeln i andra kvadranten. För att få samtliga lösningar vill vi lägga till alla vinklar som är multiplar av ett helt varv. Snurrar vi ett varv från vinkeln v kommer vi ju tillbaka till vinkeln vi och samma (x,y) koordinat som innan.

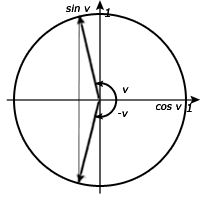
Lös ekvationen med en decimal


Eftersom vi alltid utgår ifrån punkten (1,0) så får vi här lika stort avstånd till supplementvinklarna. Den enda skillnaden är att ena är positiv och andra är negativ. Därför går det bra att svara som exemplet ovan.

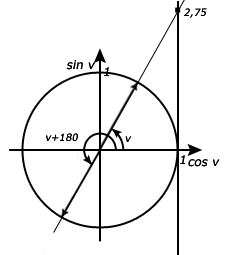
Lös ekvationen med en decimal

Detta tal löser vi precis som i det förra exemplet med tangens. Det är dock onödigt att räkna ut vinkel nummer två eftersom periodiciteten (det avstånd mellan vinklar som är samma) för tangens är n*180°, där n är ett heltal.

Lös ekvationen
a) b)

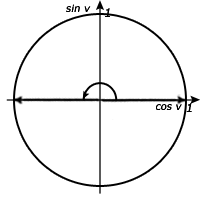
Lösning till a)
Som vi ser i figuren intill, så motsvarar vinklarna v 0° och 180° grader att sinus får värdet 0. Samtliga lösningar kommer att hittas varje gång 180° passeras. Alltså får vi svaret

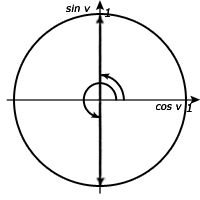
Lösning till b)
När vi tittar på ser vi att vinklarna 90° och 270° uppfyller funktionen. Även här inser vi att nästkommande lösning finns varje gång man lägger till 180°. Därför blir svaret

Bestäm nollställena till funktionen

Lösning
Nollställen räknar vi ut genom att söka det x i definitionsmängden som ger värdemängden 0, alltså



För att få fram vinkeln slår vi arcsin 0,4 på miniräknaren. Efter att vi ritat upp enhetscirkeln ser vi att det finns en supplementvinkeln som vi inte får glömma att räkna ut.
Svar
Nollställena är

Lös ekvationen och svara med en decimal.

Lösning
Vi börjar som vanligt att räkna ut vinkeln med hjälp av arcsin. Denna gång får vi vara uppmärksamma med att det inte är v vi räknar ut utan 3v!

För att få fram vad vinkeln v är så gör vi som med en vanlig ekvationen, vi delar med 3 på bägge sidor om likhetstecknet.


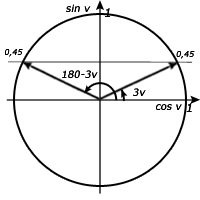
Men vi är inte riktigt färdiga än. Om vi ritar upp sin v = 0,45 i enhetscirkeln så ser vi att det finns en andra lösning i andra kvadranten och den räknar vi ut så här:

Svar
och

Lös ekvationen och svara med en decimal.

Lösning
Här stöter vi på en annorlunda typ av ekvation, men var lugn, sättet att lösa den är likadant som föregående uppgift till skillnad mot trean framför cos som vi lätt kan göra oss av med. Vi dividerar helt enkelt med 3 på båda sidor. Observera att det som står innanför sinus/cosinus/tangens ej påverkas av divisionen.

Nu har vi reducerat ekvationen till en av identisk form som vi löste innan.


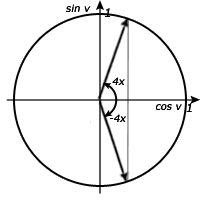
Anledningen till att det är ±70,5° ser vi tydligast då vi ritar upp 1/3 för cosinus i enhetscirkeln. Då ser vi tydligt att det finns två vinklar, en positiv och en negativ, med samma storlek som svarar mot ett och samma x-värde. Vi är ännu inte helt färdiga, utan för att räkna ut x behöver vi dividera med 4

Svar

Lös ekvationen och svara med en decimal.

Lösning
Okej, då kör vi! Nu när vi tar arccos 0,9 så är det (x-9,9°) vi räknar ut här nedan. När detta är gjort flyttar vi helt enkelt över -9,9° från den vänstra sidan till den högra. Notera att det blir ett teckenbyte då vi flyttar över från ena sidan av likhetstecknet till den andra.



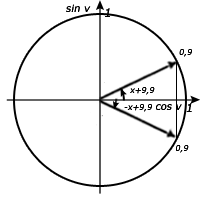
Notera även här ovan att vi har med ±25,8° på grund av att vid cosinus finns det vinklar med samma storlek med motsatt tecken som svarar mot samma x-värde.
Svar
och

Lös ekvationen

Lösning
Den kanske ser en aningen klurigare ut, men skenet bedrar. Jag lovar, detta är en baggis. Först och främst kan vi räkna ut i huvudet vad 2x+30° blir utan att först räkna ut vad sin50° blir. Detta beror på att om vi skulle slå in sin50° på miniräknaren så skulle vi få svaret 0,766…osv. Sedan, för att räkna ut vad 2x+30°, så skulle vi ju slå in arcsin0,766… och därmed få svaret 50°. Nu är vi ju tillbaka där vi började, så detta är alltså ett onödigt steg. Vi vet redan från början att 2x+30° ska bli 50°+n*360. Nedan följer fortsättningen på ekvationen.

Vi flyttar över 30° till andra sidan av likhetstecknet för att få x ensamt.



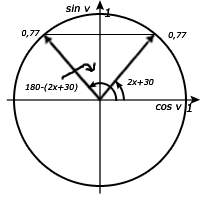
Jag börjar känna mig lite tjatig nu varje gång då jag påpekar att man ska kolla, med hjälp av enhetscirkeln, ifall det finns fler lösningar. Det ser vi i alla fall här och den andra lösningen räknar vi ut på följande vis:




Svar
och