Matte D - Trigonometriska funktioner
Trigonometriska formler
Trigonometriska ettan
Nu ska du få lära känna en ny vän. Vännen heter trigonometriska ettan, men för oss vanliga dödliga, som ständigt snubblar med tungan, är den mer känd som trig.ettan. Detta namn kommer jag att använda i mina förklaringar. Trig.ettan är ett samband mellan sin v och cos v. Vi kan använda den i en rad olika sammanhang t.ex. då vi förenklar trigonometriska uttryck eller då vi vill bestämma de exakta värdena på t.ex. cos v sin v då vi vet värdet på tan v etc.
Trigonometriska ettan inför följande enkla samband mellan cos v och sin v:
Man brukar skriva sin² v vilket är exakt samma sak som (sin v)² för att poängtera att det inte är v², utan hela uttrycket som skall kvadreras.
Ifrån trigonometriska ettan kan vi lösa ut både cos och sin enligt följande:
Visa att
Lösning
Vi börjar med att räkna ut vänsterledet:
VL
Om vi tittar på trigonometriska ettan som vi introducerades för här ovan känner vi igen vänsterledet. Vänsterleder är helt enkelt cos² x enligt trigonometriska ettan! Alltså har vi:
VL HL v.s.v.
V.s.v är en förkortning för vilket skulle visas, vilket var precis det som skulle göras i denna uppgift.
Härledning till trigonometriska ettan
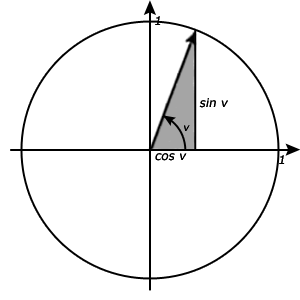
För den som vill veta så ska jag försöka med en enkel förklaring till hur trigonometriska ettan funkar. Trigonometriska ettan fungerar i princip på samma sätt som Pytagoras sats. Då vi ritar ut en vinkel eller markerar ett värde för sinus, cosinus eller tangens, så kan vi lätt rita upp en rätvinklig triangel i enhetscirkeln. Triangeln har cosinuslinjen/x-axeln som bas och visaren blir dess hypotenusa.
Det typiska utseendet för Pytagoras sats är ju a²+b²=c². Trig.ettan ser precis likadan ut förutom att bokstäverna är ersatta med sin v, cos v och 1. Det är också lite lurigt när man skriver formeln då det inte står att ettan är upphöjd till 2. Men det är bara för att 1 upphöjt till 2 är 1
Formler för motsatta vinklar v och –v
Exempel på användning av dessa formler ser du stycket här nedaför.
Formler för vinklar 180° – v och 90° – v
Exemplet nedan innefattar både stycket ”Formler för motsatta vinklar v och –v” och ”Formler för vinklar 180° – v och 90° – v”.
För en vinkel v i första kvadranten gäller att . Bestäm, utan att först räkna fram vinkeln, värdet av
a) b) c)
Lösning till a)
ftersom vi har ett värde på sin v så kan vi med hjälp av trig.ettan räkna ut vad cos v har för värde. Jag brukar ju tjata om att när man räknar med kvadratroten så får man ju ett svar som både kan vara positivt och negativt. I detta fall så vet vi att 0,8 måste vara positivt då v var en vinkel i första kvadranten. För att bestämma vad cos(180°-v) blir så tar vi hjälp av formlerna här ovan. Där ser vi att cos(180°-v) också är lika med –cos v och det hela blir så mycket enklare. Det är bara att sätta dit ett minus framför det redan uträknade cos v-värdet.
Lösning till b)
Enligt formlerna för motsatta vinklar så kan vi skriva om tan(-v) till –tan v. -tan v kan vi sedan skriva som -(sin v delat med cos v), regeln för detta hittar du i avsnittet godtyckliga vinklar. Då vi sen tidigare visste värdet på sin v och räknade ut cos v så är det bara att räkna ut divisionen.
Lösning till c)
och
I denna uppgift så börjar vi med att sätta att a=90°+v, detta för att vi ska kunna skriva att sin a=sin(180°-a). (180°-a) är ju supplementvinkeln till a och därför har de alltså samma sinusvärde.
Värdet på sin(90°+v) är alltså densamma som för supplementvinkeln sin(180°-(90°+v)). Supplementvinkeln räknar vi ut genom att ta bort parentesen runt 90°+v. Det blir då 180°-90°-v och därmed sin(90°-v). Om vi nu tittar tillbaka på våra lista med formler en bit upp på sidan så kan vi bara konstatera glatt att sin(90°-v) även kan skrivas som cos v. Värdet på detta räknade vi ju ut redan i a-uppgiften så vi svara helt enkelt 0,8.
Notera!
Det är i sådana här stunder man ska vara tacksam för att det finns så många olika formler hit och dit, de gör att talen blir så mycket enklare att lösa. Det krävs t.ex. ingen förklaring till att cos(180°-v)=-cos v, det är bara så det är. ![]()
Additionsformler
Här nedan presenteras ytterligare några formler som kan komma till användning när man ska underlätta uträkningar eller liknande.
Skriv som en summa.
Lösning
I exemplet ovan så börjar vi med att ta till regeln sin(a+b)=sin a*cos b+cos a*sin b. I din lilla formelsamling ska du nu märka ut den sida som har en tabell på de vanligaste vinklarna för cosinus och sinus samt deras värden. Tittar vi nu i den tabellen så står det att cos45° är lika med 1 delat med kvadratroten ur 2. Vi ser också att sin45° har samma värde så vi skriver ut det med. Vi gör om så många delar som möjligt till tal för att kunna räkna. Sedan bryter vi ut 1 delat med kvadratroten ur två eftersom detta tal finns både hos sin x och cos x. Och då var det klart!
Formler för dubbla vinkeln
För en vinkel i första kvadranten gäller att . Bestäm utan att beräkna vinkeln x.
Lösning
Svar
I exemplet ovan så behöver vi använda oss av regeln sin2a=2sina*cosa, men för att kunna använda den behöver vi även värdet på cos x. Det tar vi fram med hjälp av trig.ettan. Vi tecknar uttrycket för cos x och ersätter sedan sin x med det värdet som är angivet i uppgiften. Nu när vi har värdet på både sin x och cos x så är det inget som kan stoppa oss från att räkna ut vad sin2x blir. Som ni ser så behövde vi inte heller räkna ut vinkeln för att räkna ut detta.
19 maj 2010 @ 19:26
Det står sin(a – b) = sina*cosb + cosa*sinb två gånger.
19 maj 2010 @ 20:46
Oj då. Vi hade glömt den sista. Nu är alla med och ingen är med två gånger.
Tack Kaoten för att du påpekade felet.
18 oktober 2010 @ 21:48
En mycket; mycket bra sida för Den som vill fräscha upp trigonometri formlerna!
27 oktober 2010 @ 14:55
sin v=sin(v-180)
den rätt eller fel
1 november 2010 @ 13:49
Hej Ali,
“Den” är fel. Som det står lite längre upp på sidan så är sin v = sin (180-v).
18 november 2010 @ 9:13
Under exempel 2, lösning c), första raden står det
a=90-v => sin(a) = sin(180-v)
Borde det inte stå
a=90-v => sin(a) = sin(180-a)
18 november 2010 @ 15:15
Helt korrekt Oscar. Bra uppmärksammat!
Det är nu fixat, tackar!
8 februari 2011 @ 19:18
första exampet har ni inte missat ett x där 1^2 – sin^2 X ska det väl stå ?????
9 februari 2011 @ 1:29
Korrekt! Nu åtgärdat. Tackar.
22 februari 2016 @ 7:11
[...] något jag helt hade missat. Efter lite googlande så hittar jag bra förklarande exempel på matteguiden.se, samt formelsamlingen till nationella provet i Matte 4 på mattecentrums sida formelsamlingen.se. [...]