Matte Diskret - Mängdlära
Mängder
Mängder
Inom mängdlära använder man uttrycken mängd och element. För att förstå innebörden av dessa uttryck kan vi göra en jämförelse med en blomrabatt. Tänk dig att du tittar på en blomrabatt med en massa rosor. Varje ros är ett element i blomrabatten som kallas mängd.
En annan bra jämförelse är att när man befinner sig i ett rum så ser man att det finns en hel del föremål runtomkring en. Dessa föremål utgör elementen i den mängd som vi kallar rum.
Mängder brukar skrivas med versaler, stora bokstäver, och element skrivs med gemener, små bokstäver.
Inom mängdläran använder man en rad olika symboler t.ex. tillhör , och tillhör inte .
Om vi t.ex. vill säga att s är ett element i mängden A så skriver vi
(s tillhör mängden A)
Om vi t.ex. vill säga att s är inte ett element i mängden A så skriver vi
(s tillhör inte mängden A)
Om vi vill visa att mängden T består av alla heltal mellan 3 och 8 så skriver vi
eller
där “x:” innebär att man definierar x till att vara inom ett visst intervall eller att det utgör en delmängd av något.
Skriv med mängdsymboler
a) Talet tillhör de rationella talen b) Mängden D är en delmängd av mängden E
a) De rationella talen betecknas med och symbolen betyder tillhör, alltså
b) M
Svar: a) b)
Det finns en del mängder som används så ofta att de fått sina egna tecken. Exempel på dessa mängder kan vara de naturliga talen eller de reella talen.
betecknar mängden av alla naturliga tal,
betecknar mängden av alla heltal,
betecknar alla rationella tal, alltså alla tal som kan skrivas som en kvot av två
heltal t.ex.
betecknar alla reella tal t.ex.
betecknar alla komplexa tal t.ex. lösningarna till ekvationen
Den tomma mängden
Den tomma mängden innehåller inga element och betecknas då .
Ett exempel på när vi får en tom mängd är t.ex. om vi säger att A är mängden av alla heltal som är lösningar till ekvationen så är A=tomma mängden. Detta för att det inte finns någon heltalslösning till ekvationen .
Alla tomma mängder är identiska oavsett hur de “bildas”. Om B skulle vara mängden av alla negativa tal i intervallet 14 < x < 20 skulle B också vara en tom mängd eftersom det inte finns några negativa tal i intervallet 14 < x < 20.
A och B är samma mängd, den tomma mängden.
Venndiagram
Ett venndiagram kan beskrivas som att man målar upp en bild som förtydligar mängduttrycken. Grundmängden U ritas upp som en rektangel som omsluter alla delmängder som ses som slutna figurer.
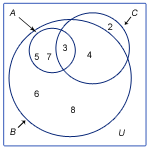Låt oss säga att
Detta skulle kunna förtydligas i ett venndiagram där man ser tydligt att A är en delmängd av B, men C är inte en delmängd av A.
Om vi endast har två mängder så kan de förhålla sig till varandra på fyra olika sätt:
1. Att D är en delmängd av E, alltså alla element som ingår i A ingår också i B. Detta skrivs som
2. Att E är en delmängd av D, alltså alla element som ingår i B ingår också i A. Detta skrivs som
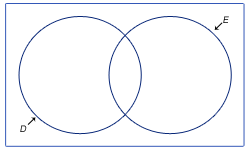
3. Att det finns element som ingår i både D och E samtidigt som det också finns element som ingår i D, men inte i E och vice versa.
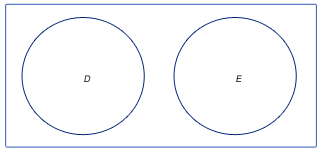
4. Eller att det inte finns några gemensamma element alls i mängderna D och E. Mängderna sägs då vara disjunkta.
Ge exempel på en mängd som är disjunkt till mängden
Då två mängder var disjunkta innebar det att de inte har några gemensamma element, alltså är det bara att ange tal som inte finns i mängden F.
Exempel på ett svar är:
Rita upp mängderna i ett venndiagram.
Först tittar vi på vilka element (siffror) som de olika mängderna har gemensamt.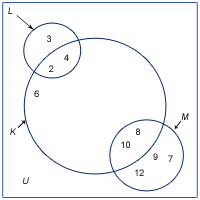 
Vi ser att K och L har siffrorna 2 och 4 gemensamt. Vi ser också att K och M har 8 och 10 gemensamt. Däremot har inte L och M några gemensamma element.
Då kan vi lämpligen rita upp mängden K i mitten med siffrorna 2 och 4 i ena hörnet där de delas med mängden L samtidigt som siffrorna 8 och 10 visas i andra hörnet där de delas med mängden M. Resterande element som är unika för mängden K skrivs enbart i cirkeln K.
Därefter ritar vi upp mängden L och M. Mängden L hade också en trea som ett element, vilket vi skriver till utanför mängden K och mängden M hade 7, 9 och 12 som ytterligare element.
Union och snitt
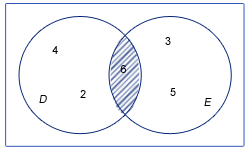Då två mängder har ett eller flera gemensamma element, t.ex. i bilden här till höger där mängderna D och E har siffran 6 är gemensamt, så säger man att snittet (skärningsmängden) av D och E är 6. Detta skrivs i symboler som och utläses A snitt B är lika med mängden som består av talet 6.
Alltså snittmängden består av de element som finns i både mängd D och E. Snittet, , representeras i figuren som den streckade delen.
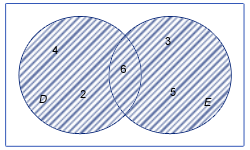
Som ni ser i figuren så finns det ju också en massa andra element förutom det gemensamma. Tillsammans omfattar mängden D och E talen 2, 3, 4, 5 och 6. Detta benämner man unionen, alltså föreningsmängden av D och E är dessa tal och detta skrivs i symboler som:
och utläses som D union E är lika med mängden av talen 2, 3, 4, 5 och 6.
Alltså består unionmängden av elementen som antingen finns i mängden D, E eller i båda mängderna. ses som den strecka delen i bilden till höger.
Bestäm a) b)
a) är snittmängden, alltså de element som mängden F och mängden G har gemensamt. Om vi tittar på de båda mängderna ser vi att de har bokstäverna d, f och g gemensamt. Alltså:
b) är föreningsmängden, alltså de element som mängden F har och de element som mängden G har var för sig, samt de element som är gemensamma. Det innebär alla bokstäver som ryms inom de båda mängderna:
Svar: a) b)
Komplementmängd
Vi säger att vi har en grundmängd, grundmängden U.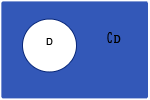 
Grundmängden U består av ett antal element och bland dem finns mängden D. Alla de element som utgör grundmängden U, men inte tillhör mängden D tillhör det så kallade komplementet till D och betecknas eller .
Alltså:
En mängd och dess komplementmängd bildar hela grundmängden tillsammans
Grundmängden U innehåller bl.a. mängden E. Vad är komplementmängden till mängden E om och ?
BILD!!
För att lösa uppgiften underlättar det mycket om vi ritar upp vad vi vet. Vi vet att vi har en grundmängd U och att den grundmängden i detta fall utgörs av alla reella tal. säger att mängden E består av alla reella tal som är mindre än 7. x:et symboliserar dessa tal och det är angett att x r en delmängd av (reella talen) och mer specifikt att x är alla de reella tal som är mindre än 7.
Eftersom E täcker in alla tal mindre än 7 så måste resterande element i grundmängden vara större än eller lika med 7 och på så vis kompletterar mängden E för att bilda grundmängden U.
Komplementmängden till E är alltså lika med alla tal större eller lika med 7 vilket skrivs så här:
Svar:
Beteckningar för olika mängder
Här tänker jag bara nämna de olika talgrupperna lite mer utförligt.
De reella talen
De reella talen innefattar alla tal, alltså den vardagliga benämningen på alla siffror oavsett om de är 1, , eller 0,4444…osv. De betecknas med bokstaven
I ingår alltså , och .
De naturliga talen
De naturliga talen betecknas med bokstaven och innefattar de positiva heltalen, alltså inga negativa tal och de har inte heller några decimaler.
Heltalen
betecknar mängden av alla heltal. Heltalen är de tal utan decimaler och de kan vara både negativa och positiva t.ex.
De rationella talen
betecknar alla rationella tal, alltså alla bråktal t.ex.
De komplexa talen
betecknar alla komplexa tal. Ett komplext tal är där a och b är reella tal och i är den imaginära enheten.
Olika beteckningar inom diskret matematik
Här vill jag bara uppmärksamma att olika matteböcker kan använda sig av olika beteckningar när det gäller vissa saker och ibland kan den skillnaden vara väsentlig.
Delmängder
Hittills har vi använt oss av tecknet när vi har velat beskriva att t.ex. A är en delmängd av B .
Men om inte delmängden A är lika med delmängden B, alltså mängderna har bara några element gemensamt, så använder en del författare istället tecknet och A sägs då vara en äkta delmängd av B. I deras sammanhang betyder då tecknet i att alla element i A också ingår i B.
Beskriva en mängd
När vi har beskrivit en mängd har vi uttryckt oss likt följande:
Men istället för kolon (:) kan man också använda semikolon (;) eller ett rakt streck (|).
Genom resterande kapitel i den diskreta matematik kommer vi att använda oss av tecknet när vi beskriver att A är en delmängd av B oavsett om de har alla eller bara några element gemensamt.
Vad gäller x: så är det just x: vi kommer att använda.
20 oktober 2011 @ 2:28
Grymt! hjälpte mig mkt! lättare att läsa och förstå än min mattebok
TACK
24 augusti 2012 @ 16:57
En hel del diskret matematik. Puhh. Nu kör vi på.
4 oktober 2012 @ 20:48
bra förklaring men kan bli bättre med flera exampel
19 november 2012 @ 12:23
underbart bra sida!
18 december 2012 @ 22:17
Innehåller inte allt , men det mesta!