Relationer
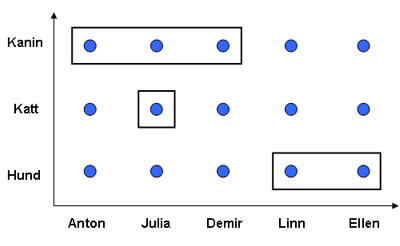
Anton, Julia, Demir, Linn och Ellen är alla djurägare. Anton och Demir har varsin kanin, Julia har en katt och Ellen och Linn har varsin hund.
Vi kan säga att det finns en relation mellan djurägarna och deras djur, och denna relation kan uttryckas som par: (Anton, kanin), (Demir, kanin), (Julia, katt), (Ellen, hund) och (Linn, hund).
Alla de möjliga kombinationerna av dessa personer och djur bildar tillsammans en mängd som vi kallar produktmängden, en produkt av mängden djurägare och mängden husdjur där respektive mängd innehåller olika element t.ex. mängden husdjur utgörs av elementen katt, hund och kanin.
Produktmängden i ovannämnda fall innehåller då element från både mängden djurägare och mängden husdjur:
(Anton, kanin), (Anton, katt), (Anton, hund)
(Demir, kanin), (Demir, katt), (Demir, hund)
(Julia, kanin), (Julia, katt), (Julia, hund)
(Ellen, kanin), (Ellen, katt), (Ellen, hund)
(Linn, kanin), (Linn, katt), (Linn, hund)
Vi kan beteckna djurägarna som mängden A och husdjuren som mängden B, produktmängden skrivs då som och innefattar då alla ordnade elementpar (a, b), alltså elementen (a) från mängden A kombineras med elementen (b) från mängden B.
De uppräknade elementen ovan visar bara alla möjliga relationer. Den verkliga relationen, alltså det faktum att vi vet att Anton och Demir har en kanin, Julia har en katt osv, är bara en delmängd av denna produktmängd.
Elementparet (Julia, Katt) tillhör därmed delmängden R och detta betyder att Julia är relaterad till Katt. Detta uttrycks matematiskt som Julia R Katt.
Man kan illustrera produktmängden i ett koordinatsystem vari man också markerar den angivna delmängden.
Vi har mängden och relationen R är given på D genom att . Ange relationen R som en delmängd av om R definieras som .
Produktmängden är alltså då vi skriver upp alla möjliga kombinationer av talen inom den angivna mängden dvs:
(11, 12), (11, 13), (11, 14), (11, 15), (11, 16),
(12, 11), (12, 13), (12, 14), (12, 15), (12, 16),
(13, 11), (13, 12), (13, 14), (13, 15), (13, 16),
(14, 11), (14, 12), (14, 13), (14, 15), (14, 16),
(15, 11), (15, 12), (15, 13), (15, 14), (15, 16),
(16, 11), (16, 12), (16, 13), (16, 14), (16, 15)
Delmängden av detta är relationen R, och R definieras som . Vi ska alltså plocka ut de kombinationerna här ovan som stämmer överens med , alltså första siffran ska vara mindre än den andra siffran vilket gäller för:
(11, 12), (11, 13), (11, 14), (11, 15), (11, 16),
(12, 13), (12, 14), (12, 15), (12, 16),
(13, 14), (13, 15), (13, 16),
(14, 15), (14, 16),
(15, 16)
Svar: {(11, 12), (11, 13), (11, 14), (11, 15), (11, 16), (12, 13), (12, 14), (12, 15), (12, 16), (13, 14), (13, 15), (13, 16), (14, 15), (14, 16), (15, 16)}
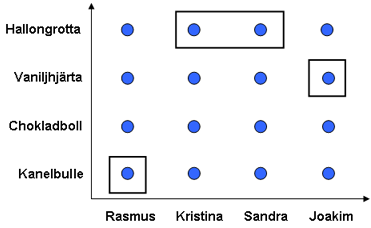
Rasmus, Kristina, Joakim och Sandra går in på ett konditori för att köpa fikabröd. På konditoriet finns endast 4 sorters kakor kvar: chokladbollar, kanelbullar, hallongrottor och vaniljhjärtan. Rasmus väljer en chokladboll, Kristina och Sandra köper varsin hallongrotta och Joakim köper ett vaniljhjärta.
Rita upp ett diagram där du anger produktmängden och sedan markerar ovannämnda relation.
Här har vi alltså fyra personer och fyra kaksorter som vi ska sätta in i ett diagram. Produktmängden visar ju alla möjliga kombinationer av personerna och kaksorterna, alltså kan man kombinera Rasmus med alla fyra kaksorter, Kristina med alla fyra kaksorter osv. Personerna är en mängd (A) och kaksorterna är en mängd (B) och produktmängden blir då . Vi ritar upp dem i ett diagram med personerna på x-axeln och kaksorterna på y-axeln:

Ovan ses koordinatsystemet med sina prickar som illustrerar de möjliga kombinationerna (relationerna), dvs hela produktmängden. Ovanstående relationer var följande:
(Rasmus, Chokladboll), (Kristina, Hallongrotta), (Sandra, Hallongrotta) och (Joakim, Vaniljhjärta). Vi markerar dessa i koordinatsystemet:
31 oktober 2011 @ 23:22
Gött med lite matte