Matte Diskret - Satslogik och algoritmer
Algoritmer
Algoritmer
En algoritm kan beskrivas som en slags instruktionslista som behövs för att lösa ett problem. Listan utgörs av en sekvens av instruktioner i en viss ordning. Det vanliga är att man har en numrerad lista. Låt säga att vi ska köra in bilen i garaget. Instruktionslistan skulle kunna se ut som följande:
- Öppna garagedörren
- Lås upp bilen
- Sätt dig i bilen och starta motorn
- Kör in bilen i garaget
För det mesta så spelar ordningen, i vilken man gör instruktionerna roll. Vi kan ju inte köra in bilen innan garagedörren är öppnad. Däremot spelar det ju ingen roll om vi låser upp bilen innan vi öppnar garagedörren. Med andra ord så kan man ibland skriva instruktionerna olika och ändå få samma resultat i slutändan.
Halvkod
Ibland kan sekvensen behöva kompletteras med s.k. halvkod. Det kan vara sekvenser som är underordnade en annan sekvens och som upprepas ett visst antal gånger innan man fortsätter med nästa rad.
T.ex.
Om man ska lägga ihop hur mycket pengar en välgörenhetsorganisation får in under en dag så måste vi ju lägga ihop alla donationer. Algoritmen kan då se ut som följande:
- Summan utgör en variabel och denna sätts till värdet 0 (vi börjar ju räkna från 0)
- För varje donation så
-
- Notera storleken på donationen
- Addera donationen till variabeln summa
- Sammanlagd donation ses hos summan
Den indragna koden är s.k. halvkod.
Det är olika slags algoritmer som utgör grunden till programmering och hur programmen fungerar som de ska. Med hjälp av olika “instruktionslistor” agerar programmet som det blir tillsagt och kan då t.ex. utföra beräkningar.
Enkel programmering
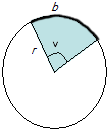 Vi ska nu programmera vår grafräknare så den kan beräkna en cirkelbåges längd åt oss. Formeln för en cirkelbåges längd kommer vi antingen ihåg från Matte B eller så tittar vi helt enkelt i formelsamlingen
Vi ska nu programmera vår grafräknare så den kan beräkna en cirkelbåges längd åt oss. Formeln för en cirkelbåges längd kommer vi antingen ihåg från Matte B eller så tittar vi helt enkelt i formelsamlingen ![]()
Längden på en cirkelbåge är:
Vi ska nu skriva en algoritm/instruktionslista på hur vi beräknar cirkelbågens längd:
- Ta reda på vinkeln hos den aktuella cirkelsektorn
- Ta reda på radien eller diametern på cirkeln
- Sätt in ovanstående värden i formeln för en cirkelbåges längd och beräkna
Steg 1. Skapa och döpa programmet.
Vi börjar med att klicka på knappen PRGM. Vi får då upp en bild som första bilden här nedan. Använd högerpilen för att gå 2 steg åt höger så vi kommer till “NEW” (se andra figuren nedan).

Genom att klicka enter kommer vi till sidan nedan där vi kan döpa programmet. Vi döper programmet till CIRKBAGE då ordet cirkelbåge inte har plats. Å, Ä, Ö finns på grafräknaren då den ör inställd på svenska, men det är inget vi går in på här.

När vi döpt programmet trycker vi ENTER och då ser det ut som nedan:
Varje kolon-tecken markerar en ny rad och de genereras automatiskt när man trycker enter för att hoppa ner en rad.
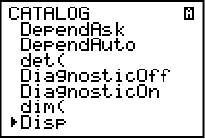
Steg 2. Skriva ut text – Kommandot “Disp”
Innan vi tittar i vår instruktionslista ovan så kan vi välja att göra så programmet visar texten “Cirkelbågens längd”. Då man vill att programmet ska visa en textsnutt ska man använda kommandot “Disp” (display = visa). Detta kommandot hittar vi i grafräknarens katalog. För att komma åt den trycker vi först på ![]() och sedan på knappen för siffra noll. Vi får då upp bilden nedan:
och sedan på knappen för siffra noll. Vi får då upp bilden nedan:
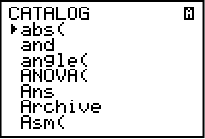
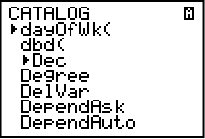
Katalogen innehåller en uppsjö av kommandon och funktioner som står i alfabetisk ordning. Om ni tittar uppe i högra hörnet på bilden så står det ett A där. A:t indikerar att grafräknaren automatiskt skriver bokstäver när du trycker på knapparna med gröna bokstäver ovanför sig. Disp börjar ju på D, så vi trycker helt enkelt på D så kommer vi direkt till orden som börjar på D. Därifrån får vi sedan bläddra nedåt med navigationspilarna tills dess att vi når Disp. Klicka på enter för att infoga Disp.

Den textsnutt som ska visas måste stå inom citationstecken (“) och nås genom att vi först trycker på den gröna bokstavsknappen ![]() och sedan knappen för plustecknet.
och sedan knappen för plustecknet.

Tips!
Istället för att sitta och klicka på alfa-knappen varje gång du ska skriva en bokstav kan du trycka ![]() och sedan
och sedan ![]() . På så vis aktiverar du funktionen “A-LOCK” dvs du låser grafräknaren i bokstavs-/textläge.
. På så vis aktiverar du funktionen “A-LOCK” dvs du låser grafräknaren i bokstavs-/textläge.
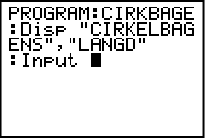
Vi skriver “cirkelbagens langd” efter citationstecknet. Problemet är att grafräknarens display inte är så bred. Det är därför bättre att skriva så ordet “langd” hamnar på andra raden när den visas. En s.k. radbrytning görs med hjälp av ett kommatecken och varje ord står inom egna citationstecken. Vi skriver “CIRKELBAGENS”,”LANGD”



Vi är nu klara med första programraden och kan nu klicka enter för att skapa en ny programrad:

Steg 3. Mata in variabler
Om vi nu tittar i vår instruktionslista vi skapade här ovan så behöver vi ta reda på vinkeln hos den aktuella cirkelsektorn. Detta är alltså information som grafräknaren behöver för att kunna beräkna cirkelbågen. För att programmet ska tillåtas ta emot information så använder vi kommandot “Input”. Detta hittar vi också i katalogen. Vi upprepar samma tillvägagångssätt som i steg 2. Gå in i katalogen, sök på I och bläddra ner till Input och infoga det med ENTER.

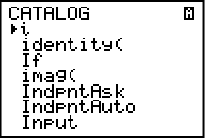
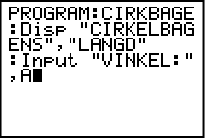
Först skriver vi en textsnutt inom citationstecken för att man ska veta vad det är programmet frågar efter. Vi skriver “VINKEL:” och därefter ett kommatecken och sedan bokstaven A. Notera att bokstaven på slutet inte behöver vara just A. Det kan vara vilken bokstav som helst, det den används till är att grafräknaren lagrar det värde man matar in på vinkeln hos denna bokstav.
När vi är klara klickar vi ENTER för att få en ny programrad. Nästa instruktion på listan är samma instruktion fast vi vill att man ska kunna mata in värdet för diametern istället. Vi upprepar alltså det vi nyss gjorde, men skriver “DIAMETER” istället för vinkel.
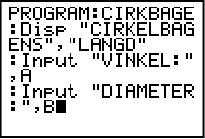
(Notera att tack vare att ordet diameter är så långt så hamnar kolontecknet man skriver in på andra raden så det ser ut som om vi har klickat ENTER för en ny programrad, men så är inte fallet).
Steg 4. Beräkna cirkelbågens längd
Om vi tittar på sista instruktionen i vår lista så står det: “Sätt in ovanstående värden i formeln för en cirkelbåges längd och beräkna”. Med andra ord så måste vi ge grafräknaren den formel vi vill att den ska beräkna. Formeln var ju och den skriver vi alltså in, men vi ersätter v med A och d med B eftersom bokstaven A får vinkeln sparad hos sig och bokstaven B får diametern sparad hos sig.
Klicka först ENTER för en ny programrad och skriv sedan in: (A/360) * π * B
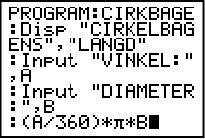
Allting man skriver sparas automatiskt, det finns ingen spara funktion. Så när vi är klara är det bara att stänga rutan genom att trycka ![]() och sedan MODE för att stänga.
och sedan MODE för att stänga.
Nu måste vi testa vårt program. Vi tar räkneexemplet från Cirkelsektorer under Matte B. Där har cirkelsektorn vinkeln 60° och radien 1 cm, vilket ger diametern 2 cm.
Gå in på PRGM och välj (klicka ENTER) CIRKBAGE i listan under EXEC. Programmet ses då för sig självt i rutan, klicka ENTER för att köra det. Vi ser då texten “Cirkelbågens längd” och ombeds ange vinkeln. Vi skriver in 60 och klickar ENTER och grafräknaren ber oss då mata in diametern. Vi skriver in 2 och klickar ENTER och vips så har grafräknaren beräknat cirkelbågens längd. Det tal vi ser på displayen stämmer överens med det resultat vi fick i räkneexemplet.

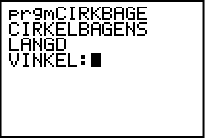
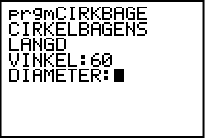
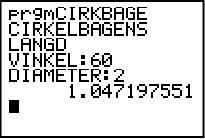
Programmet fungerar! ![]()
Program CIRKBAGE
| : Disp "CIRKELBAGENS","LÄNGD" | Visa text "Cirkelbågens längd" |
| : Input "VINKEL:",A | Mata in vinkeln |
| : Input "DIAMETER:",B | Mata in diametern |
| : (A/360) * π * B | Beräkna formeln med de an- givna värdena ovan (sparade i A och B) |
Horners metod
När vi har en funktion t.ex. och vi får veta att x = 2 så har vi lärt oss att göra följande fr att beräkna funktionens/polynomets värde:
- Ersätt alla x med 2 i funktionen
- Beräkna de olika termerna i uttrycket
- Lägg ihop alla termerna i uttrycket
Såhär blir det om vi gör som ovan:
Detta ovan är också en slags algoritm/instruktionslista som hjälper dig att lösa uppgiften. Problemet är att här blir ganska många beräkningar och det kan lätt bli fel. Vi måste göra inte mindre än 10 multiplikationer (räkna alla som görs i och med de upphöjda talen) och 4 stycken additioner eller subtraktioner, dvs totalt 14 beräkningar.
Horners metod är ett sätt att minska ner på antalet beräkningar, en funktion som används flitigt i beräkningsintensiva program.
Algoritmen går ut på att man successivt bryter ut x-faktorer ur uttrycket.
Först börjar vi med att bryta ut x ur alla termer med x i. Sjuan står redan utanför. Vi har nu gått från 10 multiplikationer till 7 multiplikationer.
Sedan fortsätter vi att bryta ut x en gång till, men denna gång gör vi det inom parentesen. Vi har nu gått från 7 multiplikationer till 5.
Vi upprepar samma sak. Bryt ut x i den innersta parentesen. Det är nu 4 multiplikationer
Nu går det inte att bryta ut x längre. Vi kan därmed stoppa in 2:an där alla x är och beräkna funktionens värde:
Bryt successivt ut x-faktorer ur polynomet
Vi börjar med att bryta ut x ur varje term, 4:an lämnas redan utanför.
Därefter kan vi bryta ut x en gång till, denna gång ur parentesen vi skapat.
Sedan är det stopp.
Svar: