Matte Diskret - Talföljder
Typer av talföljder
De finns två typer av talföljder: geometrisk och aritmetisk.
Geometrisk talföljd
Nedan ser du några olika talföljder:
5, 10, 20, 40, 80, 160
6, 60, 600, 6 000, 60 000
4, 16, 64, 256, 1024, 4096
Kan du räkna ut vilka tal som kommer härnäst i respektive talföljd?
I talföljden 5, 10, 20, 40, 80, 160 ser vi hela tiden en fördubbling av föregående talet. , , osv.
Därmed borde nästa tal vara
I talföljden 6, 60, 600, 6 000, 60 000 ser vi att varje tal multipliceras med 10.
I talföljden 4, 16, 64, 256, 1024, 4096 ser vi att varje tal multipliceras med 4.
Det som är gemensamt för alla tre talföljderna är att man utgår från ett första tal och multiplicerar detta med en konstant för att få det andra talet. Det tredje talet får man om man multiplicerar det andra talet med samma konstant, det fjärde talet om man multiplicerar det tredje talet med samma konstant osv.
Talföljder som är uppbyggda på detta sätt kallas geometriska talföljder.
Med andra ord, det som kännetecknar en geometrisk talföljd är att kvoten mellan två intilliggande tal i en talföljd är konstant. Vi tittar på talföljden 4, 16, 64, 256, 1024, 4096 igen.
Kvoten mellan 16 och 4 är 4.
Kvoten mellan 64 och 16 är 4.
Kvoten mellan 256 och 64 är 4 osv.
Kvoten är konstant.
I en geometrisk talföljd är kvoten mellan två på varandra följande element konstant
Ange de tre följande talen i den geometriska talföljden genom att bestämma kvoten i talföljden
3, 21, 147, 1029, 7203, …
Kvoten får vi fram genom att dela två intilliggande tal med varandra. T.ex.
Första talet efter 7203 får vi genom att multiplicera 7203 med 7:
Talet efter 50 421:
Talet efter 352 947:
Svar: Kvoten är 7 och de tre följande talen är 50 421, 352 947 och 2 470 629.
Att bestämma en generell beteckning för geometriska talföljder
Vi tittar åter igen på talföljden 4, 16, 64, 256, 1024, 4096, … . Låt säga att vi vill bestämma det 40:e talet i ordningen, hur gör vi då? Vi måste skriva upp en formel som kan hjälpa oss att räkna ut detta på ett enkelt sätt.
Vi börjar med att döpa talen till a1, a2, a3, a4 osv baserat på den ordningen de står i. Bokstaven motsvarar det tal som har en viss position t.ex. talföljden börjar med 2. 2:an har position 1 i talföljden och betecknas då som a1.
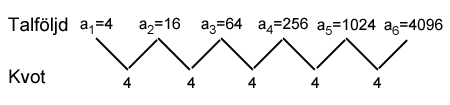
Vi ser att talet på plats 2 i talföljden får vi genom att multiplicera första talet med kvoten 4. Talet på plats 3 fås genom att multiplicera det första talet med kvoten 4 två gånger, fjärde talet genom att multiplicera det första talet med kvoten 4 tre gånger osv. Notera också i bilden att antalet differenser alltid är en färre än talets platsnummer t.ex. när vi tittar på talet 1024 som har platsnummer 5 så har vi bara passerat 4 differenser.
Vi ser alltså att om vi vill få fram det femte talet i talföljden så måste vi multiplicera det första talet med kvoten 4 fyra gånger.
Om vi nu ska generalisera så kan vi säga att talet an, som betecknar det tal med platsnummer n, är lika med första talet i talföljden (dvs 4) gånger kvoten 4 så många gånger som antalet kvoter som krävs för att få fram rätt tal. Antalet differenser är alltid 1 mindre än platsnumret därför skriver vi n-1.
Detta ger oss regeln att talet an är lika med första talet i talföljden (a1) gånger den aktuella kvoten (k) så många gånger som det finns antalet kvoter (n-1):
För en geometrisk talföljd gäller:
Bestäm i den geometriska talföljden 12, 36, 108, 324, 972, …
Genom att dela 36 med 12 ser vi att kvoten är 3:
Vi sätter in våra värden i formeln:
Svar:
I en geometrisk talföljd är och . Bestäm första talet i talföljden.
Ett hett tips om du tycker detta är lite krångligt är att rita upp talföljd med kvoten på en linje som vi gjorde ovan. Det blir lite lättare att överblicka då:
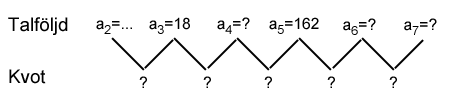
Först måste vi beräkna kvoten.
För att få fram elementet a5 multiplicerar vi element a3 med kvoten k 2 gånger. Med andra ord kan vi skriva
Vi har fått värden på både a3 och a5 så vi sätter in dessa i formeln och beräknar k.
Vi delar med 18 för att få fram k2:
Sedan tar vi roten ur på båda sidorna för att få ut k:
Nu när vi vet vår kvot kan vi sätta in det i den generella formeln för geometriska talföljder och beräkna a1 som motsvarar första talet i talföljden. an kan vara antingen a3 eller a5, det spelar ingen roll:
Vi väljer 18 och därmed får n värdet 3.
För att underlätta byter vi plats mellan höger- och vänsterled:
Vi delar med 9:
Svar: Det första elementet (a1) är 2.
Aritmetisk talföljd
Adam har bestämt sig för att träna upp sina armar genom att göra armhävningar varje dag. Första dagen börjar han med att göra 25 armhävningar. Efteråt bestämmer han sig sedan för att han varje vecka ska öka antalet armhävningar med 10 stycken. Det resulterar i att han andra veckan gör 35 armhävningar, tredje veckan 45 armhävningar, femte veckan 55 armhävningar osv.
25, 35, 45, 55, 65, ….
Skillnaden mellan antalet armhävningar varje vecka är hela tiden 10. En sådan talföljd där differensen mellan två följande tal kallas aritmetisk talföljd.
I en aritmetisk talföljd är differensen mellan två på varandra följande element konstant
Bestäm differensen i de aritmetiska talföljderna och ange de tre tal som följer de tal som visas nedan.
a) 2, 11, 20, 29, 38
b) 5, 17, 29, 41, 53
a)
Då vi redan vet att det är en aritmetisk talföljd kan vi nöja oss med att beräkna skillnaden mellan två följande tal t.ex. eller .
Differensen är alltså 9.
Nästa tal i följden är:
Talet därefter är:
Och talet efter 56 är:
b)
Vi beräknar differensen mellan två tal som följer varandra t.ex. eller .
Differensen är alltså 12.
Nästa tal i följden är:
Talet därefter är:
Och talet efter 56 är:
Svar: a) Differensen är 9 och de tre följande talen är 47, 56 och 65. b) Differensen är 12 och de tre följande talen är 65, 77 och 89.
Att bestämma en generell beteckning för aritmetiska talföljder
Låt säga att vi har en aritmetisk talföljd som ser ut som följande:
2, 4, 6, 8, 10, 12
Ganska snabbt ser vi att differensen mellan varje tal är lika med 2. Om vi nu vill räkna ut vilket tal som är nummer 20 i följden, hur gör vi då? Vi måste skriva upp en formel som kan hjälpa oss att räkna ut detta på ett enkelt sätt. Vi tittar på talföljden igen.
2, 4, 6, 8, 10, 12
Precis som innan börjar vi med att döpa talen till a1, a2, a3, a4 osv baserat på den ordningen de står i. Bokstaven motsvarar det tal som har en viss position t.ex. talföljden börjar med 2. 2:an har position 1 i talföljden och betecknas då som a1.
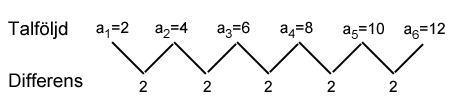
Vi ser att talet på plats 2 i talföljden får vi genom att lägga till differensen till första talet. Talet på plats 3 fås genom att lägga till två differenser till första talet, fjärde talet genom att lägga till tre differenser till första talet osv. Notera också i bilden att antalet differenser alltid är en färre än talets platsnummer t.ex. när vi tittar på talet 8 som har platsnummer 4 så har vi bara passerat 3 differenser.
Vi ser alltså att om vi vill få fram det fjärde talet i talföljden så måste vi lägga till tre differenser till talet på plats 1, alltså till talet 2.
a4 är talet på fjärde plats i ordningen, 2:an är första talet, 3:an står för antalet differenser som läggs till. 3:an multiplicerar vi med 2 eftersom 2 var differensen, vi vill ha 3 differenser.
Om vi nu ska generalisera så kan vi säga att talet an, som betecknar det tal med platsnummer n, är lika med första talet i talföljden (dvs 2) plus så många differenser som krävs för att få fram rätt tal. Antalet differenser är alltid 1 mindre än platsnumret därför skriver vi .
Detta ger oss regeln att talet an är lika med första talet i talföljden (a1) plus antalet differenser multiplicerat med differensen d (differensen varierar ju mellan olika talföljder):
För en aritmetisk talföljd gäller:
Bestäm a8 i den aritmetiska talföljden 80, 72, 64, 56, 48, …
Vi har ju formeln för aritmetiska talföljder:
Talföljden börjar med 80, alltså:
Vi beräknar differensen d:
Antalet differenser är en mindre än platsnumret vi tittar på:
Vi sätter in värdena i formeln och beräknar talet:
Svar:
I en aritmetisk talföljd är och . Bestäm första talet i talföljden.
Precis som vi gjorde innan så kan vi rita upp talföljden med differensen på en linje som vi gjorde ovan.
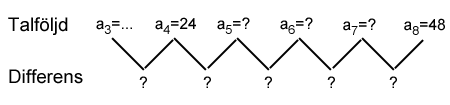
I en aritmetisk talföljd är differensen densamma hela tiden, detta kan vi utnyttja. Vi har två tal i talföljden: 24 och 48. Differensen mellan dem är . Mellan plats 4 och 8 ser vi att det är fyra differenser. Det är dessa 4 differenser som tillsammans bildar differensen på 24. Med andra ord kan vi dividera 24 med 4 för att få fram differensen:
För att få fram första talet i talföljden kan vi nyttja formeln för aritmetiska talföljder:
Vi sätter in våra värden och löser sedan ut . d står för differensen och är alltså här lika med 6. a1 är den vi ska beräkna och an kan antingen vara a4 eller a8, det spelar ingen roll.
Vi delar med minus 1 på båda sidorna för att få fram
I detta fallet blev första talet detsamma som differensen bara för att talföljden byggde på 6:ans gångertabell.
Svar: Första talet i talföljden () är 6.
Vi har talföljden 9, 16, 23, 30, …, 653. Hur många element finns det i denna talföljd?
Här kan vi återigen nyttja formeln:
Det vi vill veta är värdet på n, vilket vi kan ta reda på genom att lösa ut just n i formeln. Vi sätter in värdena vi har.
då vi går från 9 upp till detta tal.
och fås från
Vi utför multiplikationen :
Vi lägger samman 653 med -9 och +7. Därefter skiftar vi också plats på 7n och 651 för att det ser bättre ut med variabeln n på vänster sida.
Vi delar med 7 för att få fram n.
Svar: Det finns 93 element i talföljden.