Matte E - Derivator och integraler
Ändringshastighet
Om vi låter funktionen f(x) rotera kring x-axeln så bildar den en rotationskropp som vi kan beräkna volymen V av genom att använda oss av följande formel:
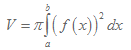
Tvärsnittsarean T(x) bildar ett cirkelområde runt x-axeln och därmed så är radien=f(x). Om vi vill beräkna tvärsnittsarean någonstans i denna kropp så använder vi oss av uttrycket:
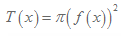
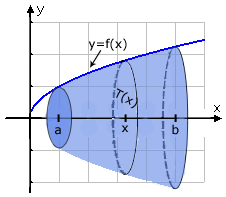
Som ni ser så är uttrycket för tvärsnittsarean derivatan av uttrycket för volymen. Vi beräknar volymen genom att göra vår funktion f(x) till en primitiv funktion. Då den deriveras är vi tillbaka på vår ursprungliga funktion som används för att räkna ut tvärsnittsarean.
Formeln för hur man räknar ut ändringshastigheten är följande:

x’(t) är uttrycket för ändringshastigheten.
För närvarande är det tyvärr så att jag inte på något enkelt sätt kan beskriva eller härleda hur man har kommit fram till detta uttryck. Personligen har jag mest accepterat att det är så det är och kommit ganska långt på det. Dock förstår jag att det vore bättre med en djupare förståelse, men tyvärr är det inget jag kan erbjuda i skrivande stund. Ni är välkomna att kontakta mig om ni har några förslag på en bra förklaring.
En närmare förklaring av uttrycket dV/dt följer här. Är det inte nödvändigt så kan ni bläddra vidare neråt till exemplet.
Hade det stått V(t) så hade det uttrycket kunnat användas för att beräkna hur stor volym vatten det fanns vid en viss tidpunkt. Deriverar vi den funktionen, (dv/dt=V’(t)), blir det istället ett uttryck för hastighet, t.ex. hur många liter (V) det fylls på per sekund (t).
Det är precis som man säger att deriverar man ett uttryck för sträckan så får man ett uttryck för hastighet:

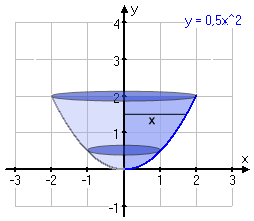
Den inre begränsningsytan av en skål är den yta som bildas då kurvan roterar kring y-axeln. Längdenheten på koordinataxlarna är 1dm. Man fyller skålen med vatten med hastigheten 0,2dm3/min. Med vilken hastighet stiger vattenytan när vattendjupet är:
a.) 0,5dm.
b.) 1,5dm.


a) Det är kurvan y=0,5x2 som ska rotera kring y-axeln. För att kunna beräkna volymen på en rotationskropp som roterar kring y-axeln måste vi skriva om funktionen där x är en funktion av y, alltså tvärtom mot vad det brukar vara.

I uppgiften frågar man alltså efter hastigheten som vattenytan stiger med vid vattendjupet 0,5 dm. Alltså vad är hastigheten då vattenytan passerar märket på y-axeln här nedanför:
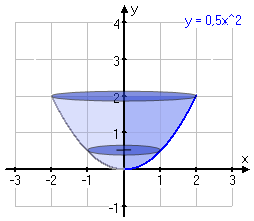
Vi ska alltså nu använda oss av uttrycket som vi tidigare nämnt.
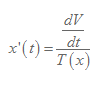
Som ni ser i diagrammet här ovanför så är ju tvärsnittet i form av en cirkel, vilket innebär att tvärsnittsarean beräknas med hjälp av formeln för en cirkels area som är:

Vi kom också fram till att uttrycket dV/dt var ett uttryck för hastighet. Och hastigheten är redan angiven eftersom texten sa att skålen fylls med vatten med hastigheten 0,2 dm3/min.

Uttrycket för vår ändringshastighet kommer alltså att bli:

För att få fram värdet på x i nämnaren bredvid pi, så tar vi helt enkelt vår omvända funktion och stoppar in värdet 0,5 på y, eftersom det gällde den vattennivån när y var lika med 0,5. På det sättet får vi fram x-värdet som, ni ser i bilden här nedanför, symboliserar radien på tvärsnittsarean.

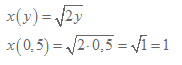
Notera att x:et i x’(t) inte har något med vårt andra x att göra.
Då vi sätter in ettan där x:et (radien) står kan vi räkna ut ändringshastigheten.
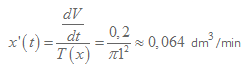
b) Den enda skillnaden här är att vi undersöker en annan höjd, nämligen 1,5 dm mot tidigare 0,5 dm. Sätt alltså y=1,5 och räkna ut x-värdet som gör att du får rätt tvärsnittsarea och därmed kan räkna ut ändringshastigheten för vattnet vid djupet 1,5 dm.

Svar: a.) 0,064 dm3/min. b.) 0,021 dm3/min.
14 januari 2011 @ 10:20
svaret på a ska väl bli ungefär 0,064 dm/ min och inte dm3/min (decimeter istället för kubikdecimeter). tack för en bra sida
24 april 2012 @ 11:48
Inte för att vara petig. Men borde inte svaren vara i dm/min istället för dm3/min?
7 maj 2012 @ 11:41
Inte egentligen, eftersom det rör sig om förändringen av bottenytan (x-led och z-led) I y-led, vilket blir 3 dimentioner <-> dm^3.
7 maj 2012 @ 14:56
*dimensioner
21 mars 2013 @ 9:38
Konstigt boken förklarade bättre än Internet!