Matte E - Differentialekvationer
Ekvationer av andra ordningen
Ekvationen y” = g(x)
Lös differentialekvationen
Detta är den enklaste inhomogena differentialekvationen av andra ordningen. Vi löser den genom att skriva de primitiva funktionerna.
Svar:
Ekvationen y” + ay’ + by = 0
Detta är en homogen differentialekvation av andra ordningen med konstanta koefficienter. Den har den allmänna lösningen:
har den allmänna lösningen:
Bestäm den lösning till för vilken y(0)=0 och y’(0)=1.
Den allmänna lösningen är
Då vi vet dessa villkor så kan vi räkna ut de två konstanterna C1 och C2:
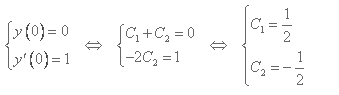
Svar:
Den allmänna lösningen
Håller ni inte med om att ekvationen ovanför liknar PQ-formeln? Visst gör den det. Och med hjälp av denna liknelse kan vi lösa ekvationen. Då vi skriver PQ-formeln använder vi oss av lite andra bokstäver:
Denna kallas för den karakteristiska ekvationen, och beroende på vad man får för svar på rötterna r1 och r2 så skiljer sig metoderna för att få fram en lösning.
1. Om den karakteristiska ekvationen har två olika rötter (reella) får differentialekvationen lösningen:
2. Om den karakteristiska ekvationens rötter är desamma och då reella (r1 = r2) är lösningen:
3. Om den karakteristiska ekvationens rötter är komplexa (i) och då varandras konjugat: så är lösningen:

27 mars 2011 @ 23:09
Jag fattar NADA…
o imorn är det prov ^.-
GAME OVER
6 april 2011 @ 20:34
Samma här….Helvete!
22 maj 2011 @ 10:07
Hur vet du att C1 blir 2? Testar du bara eller finns det någon formel?
3 augusti 2011 @ 13:37
Kajsa: Om man löser ekvationsystemet innan (m.h.a. t.ex. additionsmetoden eller substitutionsmetoden eller matriser) så får man fram vad konstanterna ska vara. Prova att sätta in värdena -2 och +2 i ekvationssystemt så får du se att det blir rätt för respektive ekvation.
31 oktober 2011 @ 13:13
Hur vet vi i andra exemplet —2 C2 = 1, alltså varför just —2 C2 ?