Matte E - Komplexa tal
Polär form
Argument
Visaren i ett komplext talplan är bestämd till längd och riktning. Längden får vi fram genom att räkna ut absolutbeloppet av z. För att räkna ut visarens riktning så behöver vi veta vinkeln mellan visaren och den positiva reella axeln. Vinkeln kallar vi (uttalas fi) och vi mäter den i antingen grader eller radianer. Vinkeln kallas argumentet för z och vi skriver arg z =
Beräkna i grader.
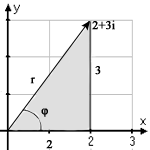
Måla upp z i ett komplext talplan för att se dess position.
Vi använder oss utav trigonometri för att lösa ut vinkeln Vi ser att det går att bilda en rätvinklig triangel med hjälp av de koordinater vi fått. Vi har alltså måtten för motstående och närliggande katet, vilket innebär att vi ska använda oss av tangens:
Många av er känner nog igen “arctan” som “tan-1“. De står för precis samma sak. Arcsin, arccos och arctan är samma som respektive sin-1 osv. Dock är det ansett ett fult och icke matematiskt korrekt skrivsätt. Arc är det korrekta. ![]()
Polär form
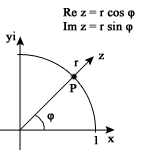
Då vi ska skriva talet z i polär form använder vi oss utav denna formel:
där motsvarar punkten P:s koordinater i enhetscirkeln och r är längden på visaren för talet z.
Skriv talet i polär form.
Absolutbeloppet:
Argumentet:
Svar:
Multiplikation och division
Då vi ska multiplicera eller dividera komplexa tal så är det ibland lättare att ha dessa tal i polär form istället för formen x + yi.
Då använder vi dessa räkneregler:
För produkten av två komplexa tal z1 och z2 gäller:
-Absolutbeloppen multipliceras:
-Argumenten adderas:
För kvoten av två komplexa tal z1 och z2 gäller:
-Absolutbeloppen divideras:
-Argumenten subtraheras:
Potensform
Detta är ännu ett sätt att skriva om z, och skrivsättet kallas potensformen för z.
De Moivres formel
de Moivres formel:
eller
gäller för alla heltalsvärden på n.
27 november 2010 @ 19:45
Angående multiplikation och division av komplexa tal i polär form. Är det inte fel tecken på “argumenten adderas” respektive “argumenten subtraheras” i rutan? Det är minus där det står addition och plus där det står subtraktion. Hälsn/Edna
28 november 2010 @ 16:03
Helt korrekt Edna. Ändrade nu, tackar!
9 mars 2011 @ 11:24
tror du glömt ett “upphöjt i n” i de moivres formel
9 mars 2011 @ 15:36
Absolut hade vi det. Tackar Stefan.
22 maj 2011 @ 23:47
Hej
Ni har råkat missa lägga ut ett minustecken framför bråket 2/4 i exempel 2 tror jag.
Tack o hej
23 maj 2011 @ 17:21
Tackar Amir! Har bytt ut hela den gamla bilden till ny text istället samt friskat upp sidan med andra stavfel och blandad white-space =)
13 april 2012 @ 15:01
kan någon hjälpa mig med följande fråga?
Givet: z1 = 2(cos 40° − I sin 40°) och z2 = 3(cos 30° + I sin 30°).
Bestäm arg (3z1 ⋅ 2z2).
_________
stämmer mina beräkningar?
3z1 = 3(2(cos 40° − I sin 40°)) = 6(cos 40° − I sin 40°).
2z2 = 2(3(cos 30° + I sin 30°)) = 6(cos 40° − I sin 40°.
6(cos 40° − I sin 40°) x 6(cos 40° − I sin 40° ger.
absolutbeloppen multiplicerade: 6×6 = 36.
arg. subtraherade: 40'-40'=0°
Svar: arg (3z1 ⋅ 2z2) = 0°.
Eller ska man räkna på annat sätt? Osäker på hur man ska utläsa detta: arg (3z1 ⋅ 2z2)..
tack för hjälpen.
13 april 2012 @ 15:01
kan någon hjälpa mig med följande fråga?
Givet: z1 = 2(cos 40° − I sin 40°) och z2 = 3(cos 30° + I sin 30°).
Bestäm arg (3z1 ⋅ 2z2).
_________
stämmer mina beräkningar?
3z1 = 3(2(cos 40° − I sin 40°)) = 6(cos 40° − I sin 40°).
2z2 = 2(3(cos 30° + I sin 30°)) = 6(cos 40° − I sin 40°.
6(cos 40° − I sin 40°) x 6(cos 40° − I sin 40° ger.
absolutbeloppen multiplicerade: 6×6 = 36.
arg. subtraherade: 40'-40'=0°
Svar: arg (3z1 ⋅ 2z2) = 0°.
Eller ska man räkna på annat sätt? Osäker på hur man ska utläsa detta: arg (3z1 ⋅ 2z2)..
tack för hjälpen.